Exam 9: Estimation Using a Single Sample
Exam 1: The Role of Statistics and the Data Analysis Process17 Questions
Exam 2: Collecting Data Sensibly39 Questions
Exam 3: Graphical Methods for Describing Data25 Questions
Exam 4: Numerical Methods for Describing Data26 Questions
Exam 5: Summarizing Bivariate Data37 Questions
Exam 6: Probability34 Questions
Exam 7: Random Variables and Probability Distributions45 Questions
Exam 8: Sampling Variability and Sampling Distributions27 Questions
Exam 9: Estimation Using a Single Sample46 Questions
Exam 10: Hypothesis Testing Using a Single Sample37 Questions
Exam 11: Comparing Two Populations or Treatments42 Questions
Exam 12: The Analysis of Categorical Data and Goodness-Of-Fit Tests21 Questions
Exam 13: Simple Linear Regression and Correlation: Inferential Methods56 Questions
Exam 14: Multiple Regression Analysis38 Questions
Exam 15: Analysis of Variance40 Questions
Exam 16: Nonparametric Distribution-Free Statistical Methods15 Questions
Select questions type
When are the population mean and the population median equal?
Free
(Multiple Choice)
4.8/5  (35)
(35)
Correct Answer:
C
A 1976 study of smokers over 30 years of age who delivered premature babies (fewer than 260 days of gestation) reported an infant survival rate of 72%. Suppose researchers would like to estimate the current survival rate. Based on the assumption that the survival rate today would be roughly similar to the survival rate in 1976, compute the sample size required to estimate the true survival proportion to within .05 with 95% confidence.
Free
(Essay)
4.8/5  (32)
(32)
Correct Answer:
Solve 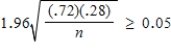 to obtain n ≥ 309.8, so a sample size of 310 or more.
to obtain n ≥ 309.8, so a sample size of 310 or more.
For a 95% confidence level, using the boundaries that capture the middle 95% of the simulated bootstrap distribution is equivalent to determining the endpoints of a confidence interval, which is represented as 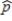 minus a number and
minus a number and 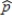 plus a number. For bootstrap confidence intervals, the number subtracted from
plus a number. For bootstrap confidence intervals, the number subtracted from 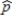 and the number added to
and the number added to 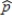 are the same.
are the same.
Free
(True/False)
4.9/5  (40)
(40)
Correct Answer:
False
Determine the confidence level associated with the given confidence interval using the standard normal curve. 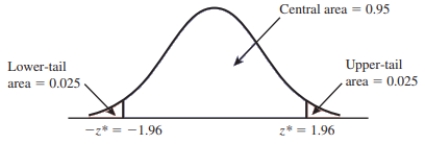
(Multiple Choice)
4.7/5  (33)
(33)
Many national parks, wildlife refuges, and wilderness areas lie directly below designated military air space. This raises issues of whether wildlife and, for example, loud jet noises are compatible. In an effort to evaluate the effects of low-altitude jet-noise, researchers simulated these noises for captive desert mule deer. Three minutes after the loud noises were played, the heart rates (beats per minute) of these animals was measured, with the following results: 55.9, 51.1, 57.5, 65.5, 68.4, 64.9, 63.1, 55.3, 63.3 Assume that it is reasonable to think that these deer can be regarded as a random sample of desert mule deer.
a) Calculate and interpret a 95% confidence interval for the mean heart rate 3 minutes after loud jet noises.
b) The mean heart rate for desert mule deer is about 51.2 beats per minute. Based on the confidence interval in part (a), do you think that the loud jet noise has some lingering effect on the heart rate of desert mule deer? Explain.
(Essay)
4.9/5  (31)
(31)
One difficulty in measuring the nesting success of birds is that the researchers must count the eggs in the nest, which is disturbing to the parents. Even though the researcher does not harm the birds, the flight of the bird might alert predators to the presence of a nest. To see if researcher activity might degrade nesting success, the nest survival of 102 nests that had their eggs counted, was recorded. Sixty-four of the nests failed (i.e. the parent abandoned the nest).
a) Construct and interpret a 95% confidence interval for the proportion of nest failures in the population.
b) The "normal" nest failure rate of these birds is 29%. Based on the confidence interval from part (a), do you think that the researcher's activity affects nesting success? Justify your answer with an appropriate statistical argument.
(Essay)
4.8/5  (31)
(31)
A random sample of the houses in a particular city is selected and the level of radon gas is measured for each house in the sample. The values collected are given below in parts per million (ppm). Experience has shown that radon gas level is approximately normally distributed for this population. 4, 8, 13, 6, 7, 3, 9, 8, 11, 8 a) Calculate a point estimate of the population mean of radon gas levels. b) Construct and interpret a 99% confidence interval for μ. c) The city standards for radon call for no more than a level of 6 ppm. From these data, does it appear that the mean radon level for city houses is under 6 ppm? Provide statistical justification for your response.
(Essay)
4.7/5  (39)
(39)
A new species of sea crab has been discovered, and an experiment conducted to determine whether or not the animal can regulate its temperature. That the animal can maintain a body temperature different from the surroundings would be considered evidence of this regulating capability. Ten of these sea crabs were exposed to ambient temperatures of 24 degrees Celsius. Their body temperatures were measured with the results below: 24.33, 24.61, 24.67, 24.64, 24.42, 24.97, 25.23, 24.73, 24.90, 24.44 For purposes of this example, assume that it is reasonable to regard these 10 crabs as a random sample from the population of all crabs of this species.
a) Calculate a point estimate of the population mean.
b) Construct and interpret a 99% confidence interval for μ.
c) Does it appear from these data that the crabs are able to regulate their body temperature? Provide statistical justification for your response.
(Essay)
5.0/5  (42)
(42)
Under what conditions is it reasonable to use the z confidence interval to estimate a population mean?
(Essay)
4.8/5  (36)
(36)
You are stuck in a long traffic jam of about 100 cars. While waiting, you talked a little to 7 drivers of the closest cars and realized that 5 of them seemed completely calm about the situation. Which method will be effective to use in order to estimate the proportion of calm people in the traffic jam and construct a confidence interval?
(Multiple Choice)
4.8/5  (37)
(37)
The composition of the earth's atmosphere may have changed over time. One attempt to discover the nature of the atmosphere long ago involved measuring the gas trapped in bubbles inside ancient amber. Amber is tree resin that has hardened and been trapped in rocks. Measurements on nine amber specimens from the late Cretaceous era (95 to 65 million years ago) give the following percentages of nitrogen: 63.4, 65.0, 64.4, 63.3, 54.8, 68.5, 60.8, 59.1, 51.0 Assume that it is reasonable to regard these trapped gas bubbles as a random sample of bubbles from the Cretaceous atmosphere.
a) Construct and interpret a 95% confidence interval for the mean percentage of nitrogen in the Cretaceous atmosphere.
b) The mean percentage of nitrogen in the atmosphere today is about 79%. Based on the confidence interval from part (a), do you think that the percentage of the atmosphere that is nitrogen has changed from the late Cretaceous era? Explain.
(Essay)
4.8/5  (34)
(34)
If we were to construct a 95% confidence interval using the method to be described shortly,
(Multiple Choice)
4.8/5  (34)
(34)
The foraging capability of Downy Woodpeckers can be compromised if part of their habitat disappears due to significant human encroachment. These creatures eat insects in trees, and if they cannot find enough food due to a decreasing forest area their body mass may decrease. A 20-year-old study of Downy Woodpeckers indicates that for male Downy Woodpeckers the average mass is about 28g, with a standard deviation of approximately 1.5g. Suppose it is desired to estimate μ, the average mass of male Downy Woodpeckers in a local forest preserve. If the 20-year-old values are taken as reasonable estimates, determine the sample size necessary to estimate μ to within 0.2 grams with 95% confidence.
(Essay)
4.7/5  (33)
(33)
In a study of termite populations in Swaziland, the following data were gathered on the percentage of termites that were classified as "major workers" at eight randomly selected sites: 37.6 20.0 28.8 29.9 51.9 13.6 34.5 29.0
a) Use the given data to produce a point estimate of μ, the true mean percentage of termites that are "major workers."
b) Use the given data to produce an unbiased point estimate of σ2, the population variance of the percentage of termites that are "major workers."
(Essay)
4.9/5  (32)
(32)
The confidence interval formula for estimating μ, that is used when n is large, is based on the Central Limit Theorem.
(True/False)
4.8/5  (35)
(35)
Over the last year, there were 80 sunny days. You can be 90% confident that the true proportion of sunny days in your life is between 0.184 and 0.255. Assume there are 365 days in a year.
(True/False)
4.8/5  (25)
(25)
The width of the one-sample confidence interval for μ decreases as the sample size grows larger.
(True/False)
4.8/5  (32)
(32)
Reading comprehension is arguably the single most important skill a student possesses. To assess the current levels of reading comprehension in 3rd grade, 25 students were randomly selected from school district class lists and given a reading comprehension test. The distribution of their scores was approximately normal with a mean of 180 and a standard deviation of 20.12. Construct a 99% confidence interval for μ, the population mean.
(Essay)
4.7/5  (42)
(42)
In a very large school district student records have been kept in three distinct data bases, one each for elementary, middle, and high school. Because of this, data entry errors tend to be compounded as students move through the grades. The district now has a new data base and wishes to fix the original data entry errors. To allocate enough secretarial time to this task, an estimate of the proportion of records that contain errors must be made. Initial estimates are that there are fixable errors in about 15% of the records. Based on the 15% assumption, compute the sample size required to estimate the true proportion of records with errors to within .025 with 95% confidence.
(Essay)
4.8/5  (31)
(31)
Showing 1 - 20 of 46
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)