Exam 19: Solution Procedures for Transportation and Assignment Problems
Exam 1: Introduction63 Questions
Exam 2: An Introduction to Linear Programming66 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution56 Questions
Exam 4: Linear Programming Applications in Marketing, Finance, and Operations Management63 Questions
Exam 5: Advanced Linear Programming Applications46 Questions
Exam 6: Distribution and Network Models70 Questions
Exam 7: Integer Linear Programming61 Questions
Exam 8: Nonlinear Optimization Models51 Questions
Exam 9: Project Scheduling: Pertcpm59 Questions
Exam 10: Inventory Models65 Questions
Exam 11: Waiting Line Models68 Questions
Exam 12: Simulation62 Questions
Exam 13: Decision Analysis97 Questions
Exam 14: Multicriteria Decisions50 Questions
Exam 15: Time Series Analysis and Forecasting63 Questions
Exam 16: Markov Processes49 Questions
Exam 17: Linear Programming: Simplex Method51 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality35 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems44 Questions
Exam 20: Minimal Spanning Tree19 Questions
Exam 21: Dynamic Programming38 Questions
Select questions type
If a transportation problem has four origins and five destinations, one of the destinations will not be fully supplied.
(True/False)
4.8/5  (34)
(34)
Explain how the Hungarian method can be used to solve an assignment problem that has a maximization objective.
(Essay)
4.9/5  (33)
(33)
After some special presentations, the employees of the AV Center have to move overhead projectors back to classrooms. The table below indicates the buildings where the projectors are now (the origins), where they need to go (the destinations), and a measure of the distance between sites. Determine the transport arrangement that minimizes the total transport distance. 
(Essay)
4.9/5  (37)
(37)
A dummy origin in a transportation problem is used when supply exceeds demand.
(True/False)
4.9/5  (33)
(33)
The transportation simplex method can be used to solve the assignment problem.
(True/False)
4.9/5  (34)
(34)
For an assignment problem where the number of agents does not equal the number of tasks, what adjustments must be made to allow the problem to be solved using the Hungarian method?
(Short Answer)
4.8/5  (35)
(35)
Al Bergman, staff traffic analyst at the corporate headquarters of Computer Products Corporation (CPC), is developing a monthly shipping plan for the El Paso and Atlanta manufacturing plants to follow next year. These plants manufacture specialized computer workstations that are shipped to five regional warehouses. Al has developed these estimated requirements and costs:  Determine how many workstations should be shipped per month from each plant to each warehouse to minimize monthly shipping costs, and compute the total shipping cost.
a.
Use the minimum cost method to find an initial feasible solution.
b.
Use the transportation simplex method to find an optimal solution.
c.
Compute the optimal total shipping cost.
Determine how many workstations should be shipped per month from each plant to each warehouse to minimize monthly shipping costs, and compute the total shipping cost.
a.
Use the minimum cost method to find an initial feasible solution.
b.
Use the transportation simplex method to find an optimal solution.
c.
Compute the optimal total shipping cost.
(Essay)
4.9/5  (30)
(30)
Explain how the transportation simplex method can be used to solve a transportation problem that has a maximization objective.
(Essay)
4.8/5  (35)
(35)
When an assignment problem involves an unacceptable assignment, a dummy agent or task must be introduced.
(True/False)
4.7/5  (32)
(32)
The per-unit change in the objective function associated with assigning flow to an unused arc in the transportation simplex method is called the
(Multiple Choice)
4.9/5  (30)
(30)
Develop the transportation tableau for this transportation problem.
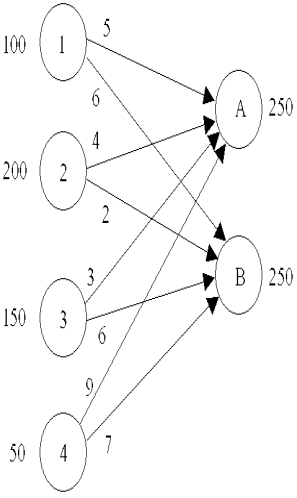
(Essay)
4.8/5  (32)
(32)
Explain what adjustments are made to the transportation tableau when total supply and total demand are not equal.
(Short Answer)
4.8/5  (23)
(23)
To use the transportation simplex method, a transportation problem that is unbalanced requires the use of
(Multiple Choice)
4.9/5  (37)
(37)
Solve the following assignment problem using the Hungarian method. No agent can be assigned to more than one task. Total cost is to be minimized.

(Essay)
4.9/5  (33)
(33)
Using the Hungarian method, the optimal solution to an assignment problem is found when the minimum number of lines required to cover the zero cells in the reduced matrix equals the number of agents.
(True/False)
5.0/5  (41)
(41)
Canning Transport is to move goods from three factories (origins) to three distribution centers (destinations). Information about the move is given below. Solve the problem using the transportation simplex method and compute the total shipping cost. 
Shipping costs are:
Shipping costs are:

(Essay)
4.8/5  (31)
(31)
For an assignment problem with 3 agents and 4 tasks, the assignment matrix will have 3 rows and 4 columns.
(True/False)
4.8/5  (33)
(33)
Consider the transportation problem below.

a.
Use the minimum cost method to find an initial feasible solution.
b.
Can the initial solution be improved?
c.
Compute the optimal total shipping cost.
a.
Use the minimum cost method to find an initial feasible solution.
b.
Can the initial solution be improved?
c.
Compute the optimal total shipping cost.
(Essay)
4.7/5  (38)
(38)
Showing 21 - 40 of 44
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)