Exam 17: Linear Programming: Simplex Method
Exam 1: Introduction63 Questions
Exam 2: An Introduction to Linear Programming66 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution56 Questions
Exam 4: Linear Programming Applications in Marketing, Finance, and Operations Management63 Questions
Exam 5: Advanced Linear Programming Applications46 Questions
Exam 6: Distribution and Network Models70 Questions
Exam 7: Integer Linear Programming61 Questions
Exam 8: Nonlinear Optimization Models51 Questions
Exam 9: Project Scheduling: Pertcpm59 Questions
Exam 10: Inventory Models65 Questions
Exam 11: Waiting Line Models68 Questions
Exam 12: Simulation62 Questions
Exam 13: Decision Analysis97 Questions
Exam 14: Multicriteria Decisions50 Questions
Exam 15: Time Series Analysis and Forecasting63 Questions
Exam 16: Markov Processes49 Questions
Exam 17: Linear Programming: Simplex Method51 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality35 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems44 Questions
Exam 20: Minimal Spanning Tree19 Questions
Exam 21: Dynamic Programming38 Questions
Select questions type
A basic feasible solution satisfies the nonnegativity restriction.
(True/False)
4.9/5  (39)
(39)
What is the criterion for entering a new variable into the basis?
(Short Answer)
4.7/5  (31)
(31)
A manager for a food company is putting together a buffet and she is trying to determine the best mix of
crab and steak to be served. Below are variable definitions she developed including vitamin, mineral and protein requirements. Also included below is an optimal simplex tableau she obtained from her
computations. She is interested in interpreting what it means.
Variable definitions:
xl = amount of crab (oz) to be served per buffet batch
x2 = amount of steak (oz) to be served per buffet batch
s1 = vitamin A units provided in excess of requirements
s2 = mineral units provided in excess of requirements
s3 = protein units provided in excess of requirements
Optimal tableau 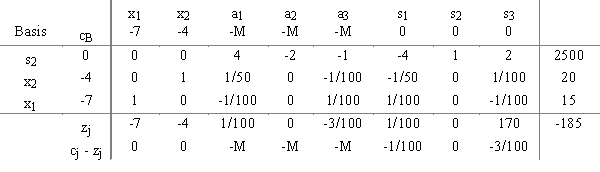
(Essay)
4.9/5  (37)
(37)
The operations research analyst for a big manufacturing firm in Oregon developed the following variable definitions for a LP maximization problem she was working on. The company was trying to determine how many consoles of each model to produce next week given each console had to go through three production departments. She obtained the following optimal simplex tableau for the problem and wanted to interpret its meaning.
Variable definitions:
xl = number of model 1 consoles produced
x2 = number of model 2 consoles produced
s1 = unused personnel hours in department 1
s2 = unused personnel hours in department 2
s3 = unused personnel hours in department 3
objective function = total profit on model 1 and model 2 consoles produced in the coming week
Optimal tableau 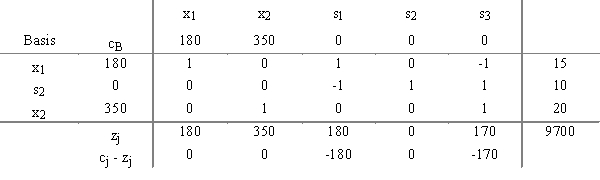
(Essay)
4.9/5  (43)
(43)
In the simplex method, a tableau is optimal only if all the cj − zj values are
(Multiple Choice)
4.7/5  (39)
(39)
What coefficient is assigned to an artificial variable in the objective function?
(Multiple Choice)
4.9/5  (38)
(38)
The values in the cj − zj , or net evaluation, row indicate
(Multiple Choice)
4.8/5  (32)
(32)
Describe and illustrate graphically the special cases that can occur in a linear programming solution. What clues for these cases does the simplex procedure supply?
(Essay)
4.9/5  (42)
(42)
The variable to remove from the current basis is the variable with the smallest positive cj − zj value.
(True/False)
4.9/5  (34)
(34)
Artificial variables are added for the purpose of obtaining an initial basic feasible solution.
(True/False)
5.0/5  (26)
(26)
An alternative optimal solution is indicated when in the simplex tableau
(Multiple Choice)
4.8/5  (30)
(30)
Write the following problem in tableau form. Which variables would be in the initial basis?
Max
x1 + 2x2
s.t.
3x1 + 4x2 ≤ 100
2x1 + 3.5x2 ≥ 60
2x1 − 1x2 = 4
x1 , x2 ≥ 0
(Essay)
4.8/5  (46)
(46)
The coefficient of an artificial variable in the objective function is zero.
(True/False)
4.8/5  (40)
(40)
Solve the following problem by the simplex method.
Max
100x1 + 120x2 + 85x3
s.t.
3x1 + 1x2 + 6x3 ≤ 120
5x1 + 8x2 + 2x3 ≤ 160
x1 , x2 , x3 ≥ 0
(Essay)
4.8/5  (37)
(37)
The variable to enter into the basis is the variable with the largest positive cj − zj value.
(True/False)
4.9/5  (33)
(33)
Infeasibility exists when one or more of the artificial variables
(Multiple Choice)
4.8/5  (36)
(36)
Which of the following is not a step that is necessary to prepare a linear programming problem for solution using the simplex method?
(Multiple Choice)
4.7/5  (39)
(39)
When a system of simultaneous equations has more variables than equations, there is a unique solution.
(True/False)
4.9/5  (36)
(36)
Showing 21 - 40 of 51
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)