Exam 9: Optimization Online Only

Determine whether the statement is true or false. -If the payoff matrix of a matrix game contains a saddle point, the optimal strategy for the row player will be to always choose the row with the largest minimum while the optimal strategy for the column player will be to always choose the column with the smallest maximum.

Solve the problem. -Anne and Michael are playing a game in which each player has a choice of two colors: green or blue. The payoff matrix with Anne as the row player is given below: 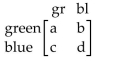Using the same payoffs for Anne and Michael, write the matrix that shows the winnings with Michael as the row player.

Find all saddle points for the matrix game. - $\left[ \begin{array} { r r r } 7 & - 4 & - 6 \\- 9 & - 8 & 8\end{array} \right]$

Find all saddle points for the matrix game. - $\left[ \begin{array} { r r } - 9 & 2 \\6 & - 2\end{array} \right]$

Write the payoff matrix for the game. -Players R and C each show 1, 2, or 3 fingers. If the total number N of fingers shown is even, then R pays N dollars to C. If N is odd, C pays N dollars to R.

Solve the problem. -Player R has two cards: a red 2 and a black 8. Player C has three cards: a red 3, a black 5, and a black 10. They each show one of their cards. If the cards are the same color, C receives the larger of The two numbers. If the cards are of different colors, R receives the sum of the two numbers. The Payoff matrix is : 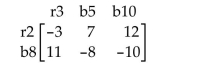Find the value of the game.

Find the value of the strategy. -Let $M$ be the matrix game having payoff matrix $\left[ \begin{array} { r r r r } 0 & 1 & - 1 & - 2 \\ 1 & 0 & 2 & 0 \\ - 1 & 2 & 0 & - 1 \end{array} \right]$ . Find $v ( \mathbf { y } )$ when $\mathbf { y } = \left[ \begin{array} { c } \frac { 1 } { 4 } \\ \frac { 1 } { 4 } \\ \frac { 1 } { 2 } \\ 0 \end{array} \right]$ .

Find the value of the matrix game. -Let $M$ be the matrix game having payoff matrix $\left[ \begin{array} { r r } 3 & - 1 \\ - 2 & 6 \end{array} \right]$ .

Find all saddle points for the matrix game. - $\left[ \begin{array} { r r r } 9 & - 2 & 5 \\2 & - 4 & - 8\end{array} \right]$

Find the expected payoff. -Let $M$ be the matrix game having payoff matrix $\left[ \begin{array} { r r r r } 0 & 3 & 1 & - 2 \\ - 3 & 0 & 2 & - 2 \\ 0 & 3 & 0 & - 2 \end{array} \right]$ . Find $\mathrm { E } ( \mathbf { x } , \mathbf { y } )$ when $\mathbf { x } = \left[ \begin{array} { c } \frac { 1 } { 4 } \\ \frac { 1 } { 2 } \\ \frac { 1 } { 4 } \end{array} \right]$ and $\mathbf { y } = \left[ \begin{array} { c } \frac { 1 } { 4 } \\ 0 \\ \frac { 1 } { 2 } \\ \frac { 1 } { 4 } \end{array} \right]$

Determine whether the statement is true or false. -In a matrix game, the value ν(y)of a particular strategy y to player C is equal to the minimum of the inner product of y with each of the rows of the payoff matrix A.

Solve the problem. -The optimal strategy for a $2 \times \mathrm { n }$ matrix game can be found as follows: obtain $\mathrm { n }$ linear functions by finding the inner product of $x ( t ) = \left[ \begin{array} { c } 1 - t \\ t \end{array} \right]$ with each of the columns of the payoff matrix A. Graph the $\mathrm { n }$ linear functions on a $\mathrm { t } - \mathrm { z }$ coordinate system. Then $v ( \mathrm { x } ( \mathrm { t } ) )$ is the minimum value of the $\mathrm { n }$ linear functions which will be seen on the graph as a polygonal path. The $z$ -coordinate of any point on this path is the minimum of the corresponding $\mathrm { z }$ coordinates of points on the $\mathrm { n }$ lines. The highest point on the path $v ( x ( t ) )$ is M. Suppose that $M$ has coordinates $( a , b )$ . What information is given by these coordinates?

Write the payoff matrix for the game. -Each player has a supply of pennies, nickels, and dimes. At a given signal, both players display one coin. If the total number of cents N is even, then R pays N cents to C. If N is odd, then C pays N cents to R.

Find the expected payoff. -Let $M$ be the matrix game having payoff matrix $\left[ \begin{array} { r r r r } 0 & 1 & - 3 & - 1 \\ 3 & 0 & 3 & 0 \\ - 3 & 3 & 0 & - 2 \end{array} \right]$ . Find $\mathrm { E } ( \mathbf { x } , \mathbf { y } )$ when $\mathbf { x } = \left[ \begin{array} { c } 0 \\ \frac { 2 } { 3 } \\ \frac { 1 } { 3 } \end{array} \right]$ and $\mathbf { y } = \left[ \begin{array} { c } \frac { 1 } { 4 } \\ \frac { 1 } { 4 } \\ \frac { 1 } { 2 } \\ 0 \end{array} \right]$

Find the value of the strategy. -Let $M$ be the matrix game having payoff matrix $\left[ \begin{array} { r r r } 1 & - 4 & 4 \\ - 1 & 1 & - 1 \\ 2 & - 2 & 0 \end{array} \right]$ . Find $v ( \mathbf { y } )$ when $\mathbf { y } = \left[ \begin{array} { c } \frac { 1 } { 4 } \\ \frac { 1 } { 2 } \end{array} \right]$

Find the optimal row or column strategy of the matrix game. -Let $M$ be the matrix game having payoff matrix $\left[ \begin{array} { r r r } 1 & - 4 & 1 \\ - 1 & 6 & 0 \\ - 6 & 3 & - 2 \end{array} \right]$ . Find the optimal column strategy.

Determine whether the statement is true or false. -If the payoff matrix of a matrix game contains a saddle point, the optimal strategy for each player will be a pure strategy.

Determine whether the statement is true or false. -The value νC of a matrix game to player C is the maximum of the values of the various possible strategies for C.

Find the optimal row or column strategy of the matrix game. -Let $\mathrm { M }$ be the matrix game having payoff matrix $\left[ \begin{array} { r r r r } 1 & 1 & - 2 & 6 \\ 0 & 4 & 5 & 3 \end{array} \right]$ . Find the optimal column strategy.

Solve the problem. -In a matrix game with payoff matrix A, how can you find the value ν(x)of a strategy x to row player R?