Exam 6: Orthogonality and Least Squares

Compute the dot product u · v. - $\mathbf { u } = \left[ \begin{array} { r } 10 \\0 \\5\end{array} \right] , \mathbf { v } = \left[ \begin{array} { r } 2 \\3 \\- 1\end{array} \right]$

Find the distance between the two vectors. - $\mathbf { u } = ( - 8 , - 1 ) , \mathbf { v } = ( 1 , - 8 )$

Find the closest point to y in the subspace W spanned by u₁ and u₂. - $\mathbf { y } = \left[ \begin{array} { r } 27 \\17 \\7\end{array} \right] , \mathbf { u } _ { 1 } = \left[ \begin{array} { r } 2 \\2 \\- 1\end{array} \right] , \mathbf { u } _ { 2 } = \left[ \begin{array} { r } - 1 \\3 \\4\end{array} \right]$

Find a least-squares solution of the inconsistent system Ax = b. - $\mathrm { A } = \left[ \begin{array} { l l } 1 & 2 \\3 & 4 \\5 & 9\end{array} \right] , \mathrm { b } = \left[ \begin{array} { l } 1 \\5 \\1\end{array} \right]$

Compute the length of the given vector. - $p ( t ) = 3 t + 4$ and $q ( t ) = 4 t - 5$ , where $t _ { 0 } = 0 , t _ { 1 } = 1 , t _ { 2 } = 2$

Find a QR factorization of the matrix A. - $A = \left[ \begin{array} { r r r } 0 & 1 & 1 \\1 & 1 & 0 \\- 1 & - 1 & 1 \\1 & - 1 & 1\end{array} \right]$

Compute the dot product u · v. - $\mathbf { u } = \left[ \begin{array} { r } - 15 \\2\end{array} \right] , \mathbf { v } = \left[ \begin{array} { r } 0 \\11\end{array} \right]$

Solve the problem. -Let $\mathrm { V }$ be in $\mathrm { P } _ { 4 }$ , involving evaluation of polynomials at $- 4 , - 1,0,1$ , and 4 , and view $\mathrm { P } _ { 2 }$ by applying the Gram-Schmidt process to the polynomials 1 , $t$ , and $t ^ { 2 }$ .

Find the distance between the two vectors. - $\mathbf { u } = ( 14,17,22 ) , \mathbf { v } = ( 2,9,2 )$

Find the distance between the two vectors. - $\mathbf { u } = ( - 5,6 , - 5 ) , \mathbf { v } = ( - 3,4,5 )$

Compute the dot product u · v. - $\mathbf { u } = \left[ \begin{array} { r } 5 \\15\end{array} \right] , \mathbf { v } = \left[ \begin{array} { r } 6 \\15\end{array} \right]$

Solve the problem. -Find the nth-order Fourier approximation to the function $f ( t ) = 3 t$ on the interval $[ 0,2 \pi ]$ .

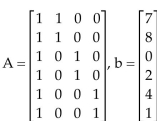
Find a least-squares solution of the inconsistent system Ax = b. -

Compute the dot product u · v. - $\mathbf { u } = \left[ \begin{array} { r } - 1 \\5 \\3\end{array} \right] , \mathbf { v } = \left[ \begin{array} { r } 3 \\2 \\- 5\end{array} \right]$

Solve the problem. -Let $\mathrm { V }$ be in $\mathrm { P } _ { 4 }$ , involving evaluation of polynomials at $- 5 , - 3,0,3$ , and 5 , and view $\mathrm { P } _ { 2 }$ by applying the Gram-Schmidt process to the polynomials $1 , t$ , and $t ^ { 2 }$ .

Solve the problem. -Data points: (5, -3), (2, 2), (4, 3), (5, 1) $\mathrm { X } = \left[ \begin{array} { l l } 1 & 5 \\1 & 2 \\1 & 4 \\1 & 5\end{array} \right] , \mathrm { y } = \left[ \begin{array} { r } - 3 \\2 \\3 \\1\end{array} \right]$

Find the orthogonal projection of y onto u. - $\mathbf { y } = \left[ \begin{array} { r } - 24 \\ 10 \end{array} \right] , \mathbf { u } = \left[ \begin{array} { r } 4 \\ 20 \end{array} \right]$

The given set is a basis for a subspace W. Use the Gram-Schmidt process to produce an orthogonal basis for W. -Let $x _ { 1 } = \left[ \begin{array} { r } 6 \\ - 3 \\ 0 \end{array} \right] , x _ { 2 } = \left[ \begin{array} { r } 6 \\ - 18 \\ 3 \end{array} \right]$

The given set is a basis for a subspace W. Use the Gram-Schmidt process to produce an orthogonal basis for W. -Let $\mathrm { x } _ { 1 } = \left[ \begin{array} { r } 0 \\ 1 \\ - 1 \\ 1 \end{array} \right] , \mathrm { x } _ { 2 } = \left[ \begin{array} { r } 1 \\ 1 \\ - 1 \\ - 1 \end{array} \right] , \mathrm { x } _ { 3 } = \left[ \begin{array} { l } 1 \\ 0 \\ 1 \\ 1 \end{array} \right]$

Determine whether the set of vectors is orthogonal. - $\left[ \begin{array} { l } - 4 \\- 8 \\- 4\end{array} \right] , \left[ \begin{array} { r } 4 \\0 \\- 4\end{array} \right] , \left[ \begin{array} { r } - 4 \\4 \\- 4\end{array} \right]$