Exam 8: Nonlinear Regression Functions

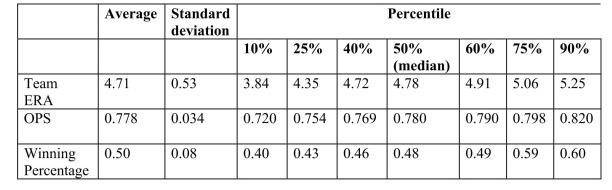
Sports economics typically looks at winning percentages of sports teams as one of various outputs, and estimates production functions by analyzing the relationship between the winning percentage and inputs.In Major League Baseball (MLB), the determinants of winning are quality pitching and batting.All 30 MLB teams for the 1999 season.Pitching quality is approximated by "Team Earned Run Average" (ERA), and hitting quality by "On Base Plus Slugging Percentage" (OPS). Summary of the Distribution of Winning Percentage, On Base Plus Slugging Percentage, and Team Earned Run Average for MLB in 1999 Your regression output is: = -0.19-0.099\times teamera +1.490\times ops ,=0.92, SER =0.02. (0.08)(0.008)(0.126) (a)Interpret the regression.Are the results statistically significant and important?

Females, it is said, make 70 cents to the dollar in the United States.To investigate this phenomenon, you collect data on weekly earnings from 1,744 individuals, 850 females and 894 males.Next, you calculate their average weekly earnings and find that the females in your sample earned $346.98, while the males made $517.70. (a)Calculate the female earnings in percent of the male earnings.How would you test whether or not this difference is statistically significant? Give two approaches.

Assume that you had data for a cross-section of 100 households with data on consumption and personal disposable income.If you fit a linear regression function regressing consumption on disposable income, what prior expectations do you have about the slope and the intercept? The slope of this regression function is called the "marginal propensity to consume." If, instead, you fit a log-log model, then what is the interpretation of the slope? Do you have any prior expectation about its size?

The figure shows is a plot and a fitted linear regression line of the age-earnings profile of 1,744 individuals, taken from the Current Population Survey. (a)Describe the problems in predicting earnings using the fitted line.What would the pattern of the residuals look like for the age category under 40?

Many countries that experience hyperinflation do not have market-determined interest rates.As a result, some authors have substituted future inflation rates into money demand equations of the following type as a proxy: $m = \beta _ { 0 } \times ( 1 + \Delta \ln P ) ^ { \beta _ { 1 } } \times e ^ { u }$ ( $m$ is real money, and $P$ is the consumer price index). Income is typically omitted since movements in it are dwarfed by money growth and the inflation rate. Authors have then interpreted $\beta _ { 1 }$ as the "semi-elasticity" of the inflation rate. Do you see any problems with this interpretation?

In nonlinear models, the expected change in the dependent variable for a change in one of the explanatory variables is given by a. $\quad \Delta Y = f \left( X _ { 1 } + \Delta X _ { 1 } , X _ { 2 } , \ldots , X _ { k } \right)$ . b. $\Delta Y = f \left( X _ { 1 } + \Delta X _ { 1 } , X _ { 2 } + \Delta X _ { 2 } , \ldots , X _ { k } + \Delta X _ { k } \right) - f \left( X _ { 1 } , X _ { 2 } , \ldots X _ { k } \right)$ . c. $\Delta Y = f \left( X _ { 1 } + \Delta X _ { 1 } , X _ { 2 } , \ldots , X _ { k } \right) - f \left( X _ { 1 } , X _ { 2 } , \ldots X _ { k } \right)$ . d. $\quad \Delta Y = f \left( X _ { 1 } + X _ { 1 } , X _ { 2 } , \ldots , X _ { k } \right) - f \left( X _ { 1 } , X _ { 2 } , \ldots X _ { k } \right)$

In the model $Y _ { i } = \beta _ { 0 } + \beta _ { 1 } X _ { 1 } + \beta _ { 2 } X _ { 2 } + \beta _ { 3 } \left( X _ { 1 } \times X _ { 2 } \right) + u _ { i }$ the expected effect $\frac { \Delta Y } { \Delta X _ { 1 } }$ is

(Requires Calculus)Show that for the log-log model the slope coefficient is the elasticity.

Choose at least three different nonlinear functional forms of a single independent variable and sketch the relationship between the dependent and independent variable.

The binary variable interaction regression

The exponential function a. is the inverse of the natural logarithm function. b. does not play an important role in modeling nonlinear regression functions in econometrics. c. can be written as $\exp \left( e ^ { x } \right)$ . d. is $e ^ { x }$ , where $e$ is $3.1415 \ldots$ .

To investigate whether or not there is discrimination against a sub-group of individuals, you regress the log of earnings on determining variables, such as education, work experience, etc., and a binary variable which takes on the value of one for individuals in that sub-group and is zero otherwise.You consider two possible specifications.First you run two separate regressions, one for the observations that include the sub-group and one for the others.Second, you run a single regression, but allow for a binary variable to appear in the regression.Your professor suggests that the second equation is better for the task at hand, as long as you allow for a shift in both the intercept and the slopes.Explain her reasoning.

In the log-log model, the slope coefficient indicates a. the effect that a unit change in $X$ has on $Y$ . b. the elasticity of $Y$ with respect to $X$ . c. $\Delta Y / \Delta X$ . d. $\frac { \Delta Y } { \Delta X } \times \frac { Y } { X }$ .

The interpretation of the slope coefficient in the model $Y _ { i } = \beta _ { 0 } + \beta _ { 1 } \ln \left( X _ { i } \right) + u _ { i }$ is as follows:

Including an interaction term between two independent variables, $X _ { 1 } \text { and } X _ { 2 } \text {, }$ allows for the following, except that:

To test whether or not the population regression function is linear rather than a polynomial of order r, a. check whether the regression $R ^ { 2 }$ for the polynomial regression is higher than that of the linear regression. b. compare the TSS from both regressions. c. look at the pattern of the coefficients: if they change from positive to negative to positive, etc., then the polynomial regression should be used. d. use the test of $( r - 1 )$ restrictions using the $F$ -statistic.

Indicate whether or not you can linearize the regression functions below so that OLS estimation methods can be applied: (a) $Y _ { i } = e ^ { \beta _ { 0 } + \beta _ { 1 } X _ { i } + u _ { i } }$

You have learned that earnings functions are one of the most investigated relationships in economics.These typically relate the logarithm of earnings to a series of explanatory variables such as education, work experience, gender, race, etc. (a)Why do you think that researchers have preferred a log-linear specification over a linear specification? In addition to the interpretation of the slope coefficients, also think about the distribution of the error term.

A polynomial regression model is specified as: a. $Y _ { i } = \beta _ { 0 } + \beta _ { 1 } X _ { i } + \beta _ { 2 } X _ { i } ^ { 2 } + \cdots + \beta _ { r } X _ { i } ^ { r } + u _ { i }$ . b. $Y _ { i } = \beta _ { 0 } + \beta _ { 1 } X _ { i } + \beta _ { 1 } ^ { 2 } X _ { i } + \cdots + \beta _ { 1 } ^ { r } X _ { i } + u _ { i }$ . c. $Y _ { i } = \beta _ { 0 } + \beta _ { 1 } X _ { i } + \beta _ { 2 } Y _ { i } ^ { 2 } + \cdots + \beta _ { r } Y _ { i } ^ { r } + u _ { i }$ . d. $Y _ { i } = \beta _ { 0 } + \beta _ { 1 } X _ { 1 i } + \beta _ { 2 } X _ { 2 } + \beta _ { 3 } \left( X _ { 1 i } \times X _ { 2 i } \right) + u _ { i }$ .

To decide whether $Y _ { i } = \beta _ { 0 } + \beta _ { 1 } X + u _ { i } \text { or } \ln \left( Y _ { i } \right) = \beta _ { 0 } + \beta _ { 1 } X + u _ { i }$ fits the data better, you cannot consult the regression R² because