Question 1

Solve the equation for x.
-$$\left| \begin{array} { l l } 
2 & 4 \
\times & 3
\end{array} \right| = - 2$$

Accepted Answer

A)  $\{ - 2 \}$ 
B)  $\{ 2 \}$ 
C)  $\{ - 1 \}$ 
D)  $\varnothing$ 
A)  $\{ - 2 \}$ 
B)  $\{ 2 \}$ 
C)  $\{ - 1 \}$ 
D)  $\varnothing$

Question 2

Solve the system by substitution.
-$$\begin{aligned}
2 x + 2 y & = 10 \
9 y & = 36 + 2 x
\end{aligned}$$

Accepted Answer

A)  $\left\{ \left( \frac { 46 } { 11 } , \frac { 9 } { 11 } \right) \right\}$ 
B)  $\left\{ \left\{ \frac { 9 } { 11 } , \frac { 108 } { 11 } \right) \right\}$ 
C)  $\left\{ \left( \frac { 9 } { 11 } , \frac { 46 } { 11 } \right) \right\}$ 
D)  $\left\{ \left\{ \frac { 9 } { 11 } , \frac { 12 } { 11 } \right) \right\}$ 
A)  $\left\{ \left( \frac { 46 } { 11 } , \frac { 9 } { 11 } \right) \right\}$ 
B)  $\left\{ \left\{ \frac { 9 } { 11 } , \frac { 108 } { 11 } \right) \right\}$ 
C)  $\left\{ \left( \frac { 9 } { 11 } , \frac { 46 } { 11 } \right) \right\}$ 
D)  $\left\{ \left\{ \frac { 9 } { 11 } , \frac { 12 } { 11 } \right) \right\}$

Question 3

Provide an appropriate response.
-Describe the elements of a $5 \times 5$ zero matrix.

Accepted Answer

A)  The matrix has zeros on the main diagonal, and all other elements are ones. 
B)  The matrix has ones on the main diagonal, and all other elements are zeros. 
C)  Every element of the matrix is zero. 
D)  The matrix has zeros on the main diagonal, and there are no restrictions on the other elements. 
A)  The matrix has zeros on the main diagonal, and all other elements are ones. 
B)  The matrix has ones on the main diagonal, and all other elements are zeros. 
C)  Every element of the matrix is zero. 
D)  The matrix has zeros on the main diagonal, and there are no restrictions on the other elements.

Question 4

Which method should be used to solve the system? Explain your answer, including a description of the first step.
-$$\begin{array} { r } 
7 x ^ { 2 } + 7 y ^ { 2 } = 81 \
- 10 x ^ { 2 } - 9 y ^ { 2 } = 49
\end{array}$$

Accepted Answer

Elimination should be used since the equ

Question 5

Find the matrix product when possible.
-Le Boulangerie, a bakery, sells four main items: sweet rolls, bread, cakes, and pies. The amount of éc 44 ingredient (in cups, except for eggs) required for these items is given by matrix A.

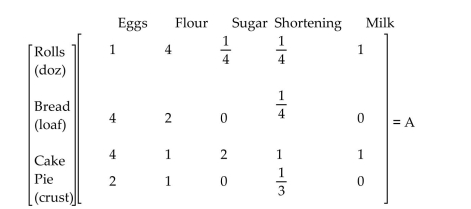The cost (in cents) for each ingredient when purchased in large lots or small lots is given in matrix B

Suppose a day's orders consist of 20 dozen sweet rolls, 200 loaves of bread, 50 cakes, and 60 pies. Us matrix multiplication to find a matrix giving the costs under the two purchase options to fill the day orders.

Accepted Answer

A)  $[ 13,36516,900 ]$ 
B)  $[ 15,01515,280 ]$ 
C)  $[ 12,10515,280 ]$ 
D)  These matrices cannot be multiplied. 
A)  $[ 13,36516,900 ]$ 
B)  $[ 15,01515,280 ]$ 
C)  $[ 12,10515,280 ]$ 
D)  These matrices cannot be multiplied.

Question 6

Give all solutions of the nonlinear system of equations, including those with nonreal complex components.
-$$\begin{array} { l } 
x ^ { 2 } + y ^ { 2 } = 113 \
x - y = 1
\end{array}$$

Accepted Answer

A)  $\{ ( 7,8 ) , ( 8,7 ) \}$ 
B)  $\{ ( 7 , - 8 ) , ( 8 , - 7 ) \}$ 
C)  $\{ ( - 7,8 ) , ( - 8,7 ) \}$ 
D)  $\{ ( - 7 , - 8 ) , ( 8,7 ) \}$ 
A)  $\{ ( 7,8 ) , ( 8,7 ) \}$ 
B)  $\{ ( 7 , - 8 ) , ( 8 , - 7 ) \}$ 
C)  $\{ ( - 7,8 ) , ( - 8,7 ) \}$ 
D)  $\{ ( - 7 , - 8 ) , ( 8,7 ) \}$

Question 7

Use a graphing calculator and the method of matrix inverses to Give five decimal places, if necessary.
-A bookstore is having a sale. All books included in the sale have a colored sticker on them to indicate the sale price. There are green stickers, red stickers, and orange stickers. Bob, Sue, and Fred each make purchases of books that are on sale. Each row of the table gives information about the numbers of book purchases and the total cost of the purchase (before taxes).
$\begin{array}{c|c|c|c|r}
\text { Person } & \text { Green } & \text { Red } & \text { Orange } & \text { Total Cost } \
\hline \text { Bob } & 1 & 2 & 2 & \$ 29.04 \
\text { Sue } & 1 & 3 & 2 & \$ 35.91 \
\text { Fred } & 1 & 2 & 3 & \$ 34.21
\end{array}$

Use this information to set up a matrix equation of the form $\mathrm { AX } = \mathrm { B }$, which can be solved to determ: the price for each type of sale book. Solve this matrix equation to find the price of a book with an ori sticker.
Use the fact that for $A = \left[ \begin{array} { l l l } 1 & 2 & 2 \ 1 & 3 & 2 \ 1 & 2 & 3 \end{array} \right] , A ^ { - 1 } = \left[ \begin{array} { r r r } 5 & - 2 & - 2 \ - 1 & 1 & 0 \ - 1 & 0 & 1 \end{array} \right]$.

Accepted Answer

A)  $\$ 5.17$ 
B)  $\$ 5.64$ 
C)  $\$ 4.81$ 
D)  $\$ 5.06$ 
A)  $\$ 5.17$ 
B)  $\$ 5.64$ 
C)  $\$ 4.81$ 
D)  $\$ 5.06$

Question 8

Graph the solution set of the system of inequalities.
-$$\begin{array} { l } 
y \geq \left( \frac { 1 } { 3 } \right) ^ { x } \
y \leq 8
\end{array}$$

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 9

Solve the system by elimination.
-$$\begin{array} { c } 
x - 3 y = 2 \
- 4 x - 2 y = - 8
\end{array}$$

Accepted Answer

A)  $\varnothing$ 
B)  $\{ ( - 2 , - 1 ) \}$ 
C)  $\{ ( 2,0 ) \}$ 
D)  $\{ ( 3,2 ) \}$ 
A)  $\varnothing$ 
B)  $\{ ( - 2 , - 1 ) \}$ 
C)  $\{ ( 2,0 ) \}$ 
D)  $\{ ( 3,2 ) \}$

Question 10

Find the value of the determinant.
-$$\left| \begin{array} { l l } 
0 & - 2 \
- 10 & 0
\end{array} \right|$$

Accepted Answer

A)  0 
B)  20 
C)  $- 20$ 
D)  $- 12$ 
A)  0 
B)  20 
C)  $- 20$ 
D)  $- 12$

Question 11

Decide whether or not the matrices are inverses of each other.
-$$\left[ \begin{array} { r r r } 
1 & - 1 & 2 \
- 3 & - 2 & 4 \
- 1 & 1 & 1
\end{array} \right] \text { and } \left[ \begin{array} { r r r } 
2 & - 1 & 0 \
- 1 & 1 & - 2 \
1 & 0 & - 1
\end{array} \right]$$

Accepted Answer

A)  Yes 
B)  No 
A)  Yes 
B)  No

Question 12

Find the partial fraction decomposition for the rational expression.
-$$\frac { 4 x ^ { 3 } + 8 x ^ { 2 } - 6 x + 2 } { 2 x ^ { 2 } - x - 1 }$$

Accepted Answer

A)  $2 x + 5 + \frac { - 7 } { 6 x + 3 } + \frac { 13 } { 3 x - 3 }$ 
B)  $2 x + 5 + \frac { - 13 } { 6 x + 3 } + \frac { 8 } { 3 x - 3 }$ 
C)  $2 x - 5 + \frac { - 13 } { 2 x + 1 } + \frac { 7 } { x - 1 }$ 
D)  $2 x - 5 + \frac { - 5 } { 6 x + 3 } + \frac { 1 } { 3 x - 3 }$ 
A)  $2 x + 5 + \frac { - 7 } { 6 x + 3 } + \frac { 13 } { 3 x - 3 }$ 
B)  $2 x + 5 + \frac { - 13 } { 6 x + 3 } + \frac { 8 } { 3 x - 3 }$ 
C)  $2 x - 5 + \frac { - 13 } { 2 x + 1 } + \frac { 7 } { x - 1 }$ 
D)  $2 x - 5 + \frac { - 5 } { 6 x + 3 } + \frac { 1 } { 3 x - 3 }$

Question 13

Write the augmented matrix for the system. Do not
-$$\begin{array} { r } 
6 x + 9 y = 3 \
5 y = 5
\end{array}$$

Accepted Answer

A) 
$\left[ \begin{array} { l l | l } 6 & 9 & 3 \ 0 & 5 & 5 \end{array} \right]$ 
B) 
$\left[ \begin{array} { l l | l } 6 & 9 & 3 \ 5 & 5 & 0 \end{array} \right]$ 
C) 
$\left[ \begin{array} { l l | l } 3 & 9 & 6 \ 5 & 0 & 5 \end{array} \right]$ 
D) 
$\left[ \begin{array} { l l | l } 5 & 0 & 5 \ 6 & 9 & 9 \end{array} \right]$ 
A) 
$\left[ \begin{array} { l l | l } 6 & 9 & 3 \ 0 & 5 & 5 \end{array} \right]$ 
B) 
$\left[ \begin{array} { l l | l } 6 & 9 & 3 \ 5 & 5 & 0 \end{array} \right]$ 
C) 
$\left[ \begin{array} { l l | l } 3 & 9 & 6 \ 5 & 0 & 5 \end{array} \right]$ 
D) 
$\left[ \begin{array} { l l | l } 5 & 0 & 5 \ 6 & 9 & 9 \end{array} \right]$

Question 14

Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, give the
solution with y arbitrary.
-$$\begin{array} { l } 
- 5 x - 3 y = - 7 \
- 15 x - 9 y = 7
\end{array}$$

Accepted Answer

A)  $\varnothing$ 
B)  $\left\{ \frac { 3 } { 4 } y + 7 , y \right\}$ 
C)  $\{ ( 3,3 ) \}$ 
D)  $\{ ( - 7,7 ) \}$ 
A)  $\varnothing$ 
B)  $\left\{ \frac { 3 } { 4 } y + 7 , y \right\}$ 
C)  $\{ ( 3,3 ) \}$ 
D)  $\{ ( - 7,7 ) \}$

Question 15

Find the inverse, if it exists, for the matrix.
-$$\left[ \begin{array} { r r r r } 
2 & - 3 & 0 & 2 \
6 & - 6 & 0 & 4 \
6 & - 12 & 0 & 6 \
0 & 0 & - 6 & 0
\end{array} \right]$$

Accepted Answer

A) 
$$\left[ \begin{array} { c c c c } 
\frac { 1 } { 2 } & - \frac { 1 } { 3 } & 0 & \frac { 1 } { 2 } \
\frac { 1 } { 6 } & - \frac { 1 } { 6 } & 0 & \frac { 1 } { 4 } \
\frac { 1 } { 6 } & - \frac { 1 } { 12 } & 0 & \frac { 1 } { 6 } \
0 & 0 & - \frac { 1 } { 6 } & 0
\end{array} \right]$$ 
B)  The inverse does not exist. 
C) 
$\left[\begin{array}{rrrr}
-1 & \frac{1}{2} & 0 & 0 \
1 & 0 & -\frac{1}{3} & 0 \
0 & 0 & 0 & -\frac{1}{6} \
3&-\frac{1}{2} & -\frac{1}{2} & 0
\end{array}\right]$ 
D) 
$\left[\begin{array}{rrrr}
-1 & 1 & 0 & 3 \
\frac{1}{2} & 0 & 0 & -\frac{1}{2} \
0 & -\frac{1}{3} & 0 & -\frac{1}{2} \
0 & 0 & -\frac{1}{6} & 0
\end{array}\right]$ 
A) 
$$\left[ \begin{array} { c c c c } 
\frac { 1 } { 2 } & - \frac { 1 } { 3 } & 0 & \frac { 1 } { 2 } \
\frac { 1 } { 6 } & - \frac { 1 } { 6 } & 0 & \frac { 1 } { 4 } \
\frac { 1 } { 6 } & - \frac { 1 } { 12 } & 0 & \frac { 1 } { 6 } \
0 & 0 & - \frac { 1 } { 6 } & 0
\end{array} \right]$$ 
B)  The inverse does not exist. 
C) 
$\left[\begin{array}{rrrr}
-1 & \frac{1}{2} & 0 & 0 \
1 & 0 & -\frac{1}{3} & 0 \
0 & 0 & 0 & -\frac{1}{6} \
3&-\frac{1}{2} & -\frac{1}{2} & 0
\end{array}\right]$ 
D) 
$\left[\begin{array}{rrrr}
-1 & 1 & 0 & 3 \
\frac{1}{2} & 0 & 0 & -\frac{1}{2} \
0 & -\frac{1}{3} & 0 & -\frac{1}{2} \
0 & 0 & -\frac{1}{6} & 0
\end{array}\right]$

Question 16

Find the inverse, if it exists, for the matrix.
-$$\left[ \begin{array} { r r } 
6 & 0 \
- 5 & 3
\end{array} \right]$$

Accepted Answer

A) 
$$\left[ \begin{array} { r r } 
\frac { 1 } { 6 } & 0 \
- \frac { 5 } { 18 } & \frac { 1 } { 3 }
\end{array} \right]$$ 
B)

$$\left[ \begin{array} { c c } 
\frac { 1 } { 6 } & 0 \
\frac { 5 } { 18 } & \frac { 1 } { 3 }
\end{array} \right]$$ 
C) 
$$\left[ \begin{array} { c c } 
\frac { 1 } { 3 } & 0 \
\frac { 5 } { 18 } & \frac { 1 } { 6 }
\end{array} \right]$$ 
D)  The inverse does not exist. 
A) 
$$\left[ \begin{array} { r r } 
\frac { 1 } { 6 } & 0 \
- \frac { 5 } { 18 } & \frac { 1 } { 3 }
\end{array} \right]$$ 
B)

$$\left[ \begin{array} { c c } 
\frac { 1 } { 6 } & 0 \
\frac { 5 } { 18 } & \frac { 1 } { 3 }
\end{array} \right]$$ 
C) 
$$\left[ \begin{array} { c c } 
\frac { 1 } { 3 } & 0 \
\frac { 5 } { 18 } & \frac { 1 } { 6 }
\end{array} \right]$$ 
D)  The inverse does not exist.

Question 17

Decide whether or not the matrices are inverses of each other.
-$$\left[ \begin{array} { r r } 
- 2 & 4 \
4 & - 4
\end{array} \right] \text { and } \left[ \begin{array} { c c } 
\frac { 1 } { 2 } & \frac { 1 } { 4 } \
\frac { 1 } { 2 } & \frac { 1 } { 4 }
\end{array} \right]$$

Accepted Answer

A)  Yes 
B)  No 
A)  Yes 
B)  No

Question 18

Use Cramer's rule to solve the system of equations. If D = 0, use another method to determine the solution set.
-$$\begin{array} { l } 
9 x + 5 y = - 38 \
- 7 x - 2 y = 39
\end{array}$$

Accepted Answer

A)  Cramer's rule does not apply since $D = 0$; $\varnothing$ 
B)  $\{ ( - 8,6 ) \}$ 
C)  $\{ ( - 7,6 ) \}$ 
D)  $\{ ( - 7,5 ) \}$ 
A)  Cramer's rule does not apply since $D = 0$; $\varnothing$ 
B)  $\{ ( - 8,6 ) \}$ 
C)  $\{ ( - 7,6 ) \}$ 
D)  $\{ ( - 7,5 ) \}$

Question 19

Find the partial fraction decomposition for the rational expression.
-$$\frac { 7 x ^ { 2 } + 32 x - 9 } { \left( 2 x ^ { 2 } + 1 \right) ( 4 - x ) }$$

Accepted Answer

A)  $\frac { 237 x - 108 } { 2 x ^ { 2 } + 1 } + \frac { - 135 } { x - 4 }$ 
B)  $\frac { 7 x - 4 } { 2 x ^ { 2 } + 1 } + \frac { 7 } { x - 4 }$ 
C)  $\frac { 237 x + 108 } { 2 x ^ { 2 } + 1 } + \frac { - 135 } { x - 4 }$ 
D)  $\frac { 7 x - 4 } { 2 x ^ { 2 } + 1 } + \frac { - 7 } { x - 4 }$ 
A)  $\frac { 237 x - 108 } { 2 x ^ { 2 } + 1 } + \frac { - 135 } { x - 4 }$ 
B)  $\frac { 7 x - 4 } { 2 x ^ { 2 } + 1 } + \frac { 7 } { x - 4 }$ 
C)  $\frac { 237 x + 108 } { 2 x ^ { 2 } + 1 } + \frac { - 135 } { x - 4 }$ 
D)  $\frac { 7 x - 4 } { 2 x ^ { 2 } + 1 } + \frac { - 7 } { x - 4 }$

Question 20

Use a graphing calculator to Express solutions with approximations to the nearest thousandth.
-$$\begin{array} { l } 
3 x + 4 y + z = 6 \
3 x - 3 y - z = 22 \
5 x + y + 4 z = 19
\end{array}$$

Accepted Answer

A)  $\{ ( - 1 , - 2,5 ) \}$ 
B)  $\{ ( 5 , - 2 , - 1 ) \}$ 
C)  $\varnothing$ 
D)  $\{ ( 5 , - 1 , - 2 ) \}$ 
A)  $\{ ( - 1 , - 2,5 ) \}$ 
B)  $\{ ( 5 , - 2 , - 1 ) \}$ 
C)  $\varnothing$ 
D)  $\{ ( 5 , - 1 , - 2 ) \}$

Solve the equation for x. - $\left| \begin{array} { l l } 2 & 4 \\\times & 3\end{array} \right| = - 2$

Solve the system by substitution. - 2x+2y =10 9y =36+2x

Provide an appropriate response. -Describe the elements of a $5 \times 5$ zero matrix.

Which method should be used to solve the system? Explain your answer, including a description of the first step. - 7+7=81 -10-9=49

Give all solutions of the nonlinear system of equations, including those with nonreal complex components. - +=113 x-y=1

Graph the solution set of the system of inequalities. - y\geq y\leq8 $Graph the solution set of the system of inequalities. - \begin{array} { l } y \geq \left( \frac { 1 } { 3 } \right) ^ { x } \\ y \leq 8 \end{array}$

Solve the system by elimination. - x-3y=2 -4x-2y=-8

Find the value of the determinant. - $\left| \begin{array} { l l } 0 & - 2 \\- 10 & 0\end{array} \right|$

Decide whether or not the matrices are inverses of each other. - $\left[ \begin{array} { r r r } 1 & - 1 & 2 \\- 3 & - 2 & 4 \\- 1 & 1 & 1\end{array} \right] \text { and } \left[ \begin{array} { r r r } 2 & - 1 & 0 \\- 1 & 1 & - 2 \\1 & 0 & - 1\end{array} \right]$

Find the partial fraction decomposition for the rational expression. - $\frac { 4 x ^ { 3 } + 8 x ^ { 2 } - 6 x + 2 } { 2 x ^ { 2 } - x - 1 }$

Write the augmented matrix for the system. Do not - 6x+9y=3 5y=5

Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, give the solution with y arbitrary. - -5x-3y=-7 -15x-9y=7

Find the inverse, if it exists, for the matrix. - $\left[ \begin{array} { r r r r } 2 & - 3 & 0 & 2 \\6 & - 6 & 0 & 4 \\6 & - 12 & 0 & 6 \\0 & 0 & - 6 & 0\end{array} \right]$

Find the inverse, if it exists, for the matrix. - $\left[ \begin{array} { r r } 6 & 0 \\- 5 & 3\end{array} \right]$

Decide whether or not the matrices are inverses of each other. - $\left[ \begin{array} { r r } - 2 & 4 \\4 & - 4\end{array} \right] \text { and } \left[ \begin{array} { c c } \frac { 1 } { 2 } & \frac { 1 } { 4 } \\\frac { 1 } { 2 } & \frac { 1 } { 4 }\end{array} \right]$

Use Cramer's rule to solve the system of equations. If D = 0, use another method to determine the solution set. - 9x+5y=-38 -7x-2y=39

Find the partial fraction decomposition for the rational expression. - $\frac { 7 x ^ { 2 } + 32 x - 9 } { \left( 2 x ^ { 2 } + 1 \right) ( 4 - x ) }$

Use a graphing calculator to Express solutions with approximations to the nearest thousandth. - 3x+4y+z=6 3x-3y-z=22 5x+y+4z=19

Review of Basic Concepts

Equations and Inequalities

Graphs and Functions

Polynomial and Rational Functions

Inverse, Exponential, and Logarithmic Functions

Trigonometric Functions

The Circular Functions and Their Graphs

Trigonometric Identities and Equations

Applications of Trigonometry

Analytic Geometry

Further Topics in Algebra

Filters

Exam 10: Systems and Matrices

Solve the equation for x. - ∣24×3∣=−2\left| \begin{array} { l l } 2 & 4 \\\times & 3\end{array} \right| = - 2​2×​43​​=−2