Solve the system in terms of the arbitrary variable x. -\[\begin{array} { l } x - 6 y + z = 10 \\ 6 x - y - z = 18 \end{array}\]

A) $\{ ( x , x - 4,6 x - 14 ) \}$ B) $\{ ( x , x - 4,5 x ) \}$ C) $\{ ( x , x - 4,5 x - 14 ) \}$ D) $\{ ( 0 , - 4 , - 14 ) \}$ A) $\{ ( x , x - 4,6 x - 14 ) \}$ B) $\{ ( x , x - 4,5 x ) \}$ C) $\{ ( x , x - 4,5 x - 14 ) \}$ D) $\{ ( 0 , - 4 , - 14 ) \}$

Write the augmented matrix for the system. Do not -\[\begin{array} { c } 5 x + 5 y + 7 z = 23 \\ - 2 x + 9 y + 4 z = 6 \\ 2 x + 5 y + 2 z = 16 \end{array}\]

A) \[\left[ \begin{array} { r r r | r } 5 & 5 & 7 & 23 \\ - 2 & 9 & 4 & 6 \\ 2 & 5 & 2 & 16 \end{array} \right]\] B) \[\left[ \begin{array} { r r r | r } 5 & - 2 & 2 & 23 \\ 5 & 9 & 5 & 6 \\ 7 & 4 & 2 & 16 \end{array} \right]\] C) \[\left[ \begin{array} { r r r } 5 & 5 & 7 \\ - 2 & 9 & 4 \\ 2 & 5 & 2 \end{array} \right]\] D) \[\left[ \begin{array} { r r r | r } 23 & 7 & 5 & 5 \\ 6 & 4 & 9 & - 2 \\ 16 & 2 & 5 & 2 \end{array} \right]\] A) \[\left[ \begin{array} { r r r | r } 5 & 5 & 7 & 23 \\ - 2 & 9 & 4 & 6 \\ 2 & 5 & 2 & 16 \end{array} \right]\] B) \[\left[ \begin{array} { r r r | r } 5 & - 2 & 2 & 23 \\ 5 & 9 & 5 & 6 \\ 7 & 4 & 2 & 16 \end{array} \right]\] C) \[\left[ \begin{array} { r r r } 5 & 5 & 7 \\ - 2 & 9 & 4 \\ 2 & 5 & 2 \end{array} \right]\] D) \[\left[ \begin{array} { r r r | r } 23 & 7 & 5 & 5 \\ 6 & 4 & 9 & - 2 \\ 16 & 2 & 5 & 2 \end{array} \right]\]

Solve the system by substitution. -\[\begin{array} { l } - 2 x = 5 y + 19 \\ - 31 = 6 y - 3 x \end{array}\]

A) $\left\{ \left( \frac { 7 } { 6 } , - \frac { 119 } { 27 } \right) \right\}$ B) $\left\{ \left\{ - \frac { 41 } { 27 } , - \frac { 119 } { 27 } \right) \right\}$ C) $\left\{ \left( - \frac { 119 } { 27 } , \frac { 41 } { 27 } \right) \right\}$ D) $\left\{ \left\{ \frac { 41 } { 27 } , - \frac { 119 } { 27 } \right] \right\}$ A) $\left\{ \left( \frac { 7 } { 6 } , - \frac { 119 } { 27 } \right) \right\}$ B) $\left\{ \left\{ - \frac { 41 } { 27 } , - \frac { 119 } { 27 } \right) \right\}$ C) $\left\{ \left( - \frac { 119 } { 27 } , \frac { 41 } { 27 } \right) \right\}$ D) $\left\{ \left\{ \frac { 41 } { 27 } , - \frac { 119 } { 27 } \right] \right\}$

Exam 10: Systems and Matrices

Solve the problem. -Michael's bank contains only nickels, dimes, and quarters. There are 51 coins in all, valued at \$4.15. The number of nickels is 5 short of being three times the sum of the number of dimes and quarters. How many dimes are in the bank?

(Multiple Choice)

4.9/5

(37)

Question 21

Provide an appropriate response. -Suppose that you are solving a system of three linear equations by the Gauss-Jordan method and obtain the following augmented matrix. $\left[ \begin{array} { r r r | r } 1 & - 7 & 11 & - 30 \\0 & 0 & 0 & 0 \\0 & 18 & - 3 & 26\end{array} \right]$ What conclusion can you draw about the solutions of the system?

(Multiple Choice)

4.7/5

(43)

Question 22

Solve the equation for x. - $\left| \begin{array} { r r } - 2 & 5 \\1 & x\end{array} \right| = - 3$

(Multiple Choice)

4.9/5

(40)

Question 23

Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, give the solution with y arbitrary. - 2x+5y=-7 -6x-15y=21

(Multiple Choice)

4.8/5

(37)

Question 24

Provide an appropriate response. -Suppose that $A$ and $B$ are two matrices such that $A + B , A - B$ , and $A B$ all exist. What can you conclude about the dimensions of $\mathrm { A }$ and $\mathrm { B }$ ?

(Multiple Choice)

4.9/5

(34)

Question 25

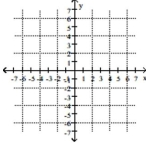
Graph the solution set of the system of inequalities. - y\leq--6x-4 y\geq+6x+4 $Graph the solution set of the system of inequalities. - \begin{array} { l } y \leq - x ^ { 2 } - 6 x - 4 \\ y \geq x ^ { 2 } + 6 x + 4 \end{array}$

(Multiple Choice)

4.7/5

(40)

Question 26

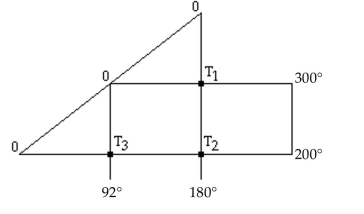
Solve the problem using matrices. -In a study of heat transfer in a grid of wires, the temperature at an exterior node is maintained at a constant value (in ${ } ^ { \circ } \mathrm { F }$ ) as shown in the figure. When the grid is in thermal equilibrium, the temperature at an interior node is the average of the temperatures at the four adjacent nodes. For instance $T _ { 1 } = \frac { 0 + 0 + 300 + T _ { 2 } } { 4 }$ , or $4 T _ { 1 } - T _ { 2 } = 300$ . Find the temperatures $T _ { 1 } , T _ { 2 }$ , and $T _ { 3 }$ when the grid is in thermal equilibrium. $Solve the problem using matrices. -In a study of heat transfer in a grid of wires, the temperature at an exterior node is maintained at a constant value (in { } ^ { \circ } \mathrm { F } ) as shown in the figure. When the grid is in thermal equilibrium, the temperature at an interior node is the average of the temperatures at the four adjacent nodes. For instance T _ { 1 } = \frac { 0 + 0 + 300 + T _ { 2 } } { 4 } , or 4 T _ { 1 } - T _ { 2 } = 300 . Find the temperatures T _ { 1 } , T _ { 2 } , and T _ { 3 } when the grid is in thermal equilibrium.$

(Multiple Choice)

4.9/5

(37)

Question 27

Provide an appropriate response. -Describe the characteristics of an augmented matrix in diagonal or reduced-row echelon form. 141)

(Multiple Choice)

4.9/5

(36)

Question 28

Provide an appropriate response. -What is the value of $\left| \begin{array} { l l l } \mathrm { m } & \mathrm { n } & \mathrm { p } \\0 & 0 & 0 \\\mathrm { q } & \mathrm { r } & \mathrm { s }\end{array} \right|$ for any values of the variables?

(Multiple Choice)

4.8/5

(42)

Question 29

Solve the system in terms of the arbitrary variable x. - x-6y+z=10 6x-y-z=18

(Multiple Choice)

4.9/5

(38)

Question 30

Use a graphing calculator and the method of matrix inverses to Give five decimal places, if necessary. -A company makes 3 types of cable. Cable A requires 3 black, 3 white, and 2 red wires. B requires 1 black, 2 white, and 1 red. C requires 2 black, 1 white, and 2 red. The company used 95 black, 100 white and 90 red wires. How many of each type of cable were made?

(Multiple Choice)

4.8/5

(41)

Question 31

Solve the problem. -A $\$ 178,000$ trust is to be invested in bonds paying $7 \%$ , CDs paying $6 \%$ , and mortgages paying $9 \%$ . The bond and CD investment together must equal the mortgage investment. To earn a $\$ 13,750$ annual income from the investments, how much should the bank invest in bonds?

(Multiple Choice)

4.7/5

(41)

Question 32

Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, give the solution with y arbitrary. - 4x+3y=1 2x+4y=8

(Multiple Choice)

4.8/5

(28)

Question 33

Write the augmented matrix for the system. Do not - 5x+5y+7z=23 -2x+9y+4z=6 2x+5y+2z=16

(Multiple Choice)

4.8/5

(41)

Question 34

Solve the linear programming problem. -A summer camp wants to hire counselors and aides to fill its staffing needs at minimum cost. The average monthly salary of a counselor is $2400, and the average monthly salary of an aide is $1100. The camp can accommodate up to 35 staff members and needs at least 20 to run properly. The Camp must have at least 10 aides and may have up to 3 aides for every 2 counselors. How many Counselors and how many aides should the camp hire to minimize cost?

(Multiple Choice)

5.0/5

(45)

Question 35

Find the partial fraction decomposition for the rational expression. - $\frac { x ^ { 2 } } { x ^ { 2 } + 6 x + 9 }$

(Multiple Choice)

4.8/5

(45)

Question 36

If the system has infinitely many solutions, write the solution set with x arbitrary. - 7x-6y=1 -14x+12y=1

(Multiple Choice)

4.9/5

(47)

Question 37

Find the partial fraction decomposition for the rational expression. - $\frac { 4 x ^ { 3 } + 8 x ^ { 2 } + 5 x - 7 } { 2 x ^ { 2 } - x - 1 }$

(Multiple Choice)

4.9/5

(37)

Question 38

Find the values of the variables for which the statement is true, if possible. - $\left[ \begin{array} { l l l } - 2 & b & 4 \end{array} \right] + \left[ \begin{array} { l l l } a & 8 & c \end{array} \right] = \left[ \begin{array} { l l l } 5 & - 1 & 4 \end{array} \right]$

(Multiple Choice)

4.9/5

(47)

Question 39

Solve the system by substitution. - -2x=5y+19 -31=6y-3x

(Multiple Choice)

4.8/5

(34)

Question 40

Showing 21 - 40 of 507

Solve the problem. -Michael's bank contains only nickels, dimes, and quarters. There are 51 coins in all, valued at \$4.15. The number of nickels is 5 short of being three times the sum of the number of dimes and quarters. How many dimes are in the bank?

Solve the equation for x. - $\left| \begin{array} { r r } - 2 & 5 \\1 & x\end{array} \right| = - 3$

Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, give the solution with y arbitrary. - 2x+5y=-7 -6x-15y=21

Provide an appropriate response. -Suppose that $A$ and $B$ are two matrices such that $A + B , A - B$ , and $A B$ all exist. What can you conclude about the dimensions of $\mathrm { A }$ and $\mathrm { B }$ ?

Graph the solution set of the system of inequalities. - y\leq--6x-4 y\geq+6x+4 $Graph the solution set of the system of inequalities. - \begin{array} { l } y \leq - x ^ { 2 } - 6 x - 4 \\ y \geq x ^ { 2 } + 6 x + 4 \end{array}$

Provide an appropriate response. -Describe the characteristics of an augmented matrix in diagonal or reduced-row echelon form. 141)

Provide an appropriate response. -What is the value of $\left| \begin{array} { l l l } \mathrm { m } & \mathrm { n } & \mathrm { p } \\0 & 0 & 0 \\\mathrm { q } & \mathrm { r } & \mathrm { s }\end{array} \right|$ for any values of the variables?

Solve the system in terms of the arbitrary variable x. - x-6y+z=10 6x-y-z=18

Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, give the solution with y arbitrary. - 4x+3y=1 2x+4y=8

Write the augmented matrix for the system. Do not - 5x+5y+7z=23 -2x+9y+4z=6 2x+5y+2z=16

Find the partial fraction decomposition for the rational expression. - $\frac { x ^ { 2 } } { x ^ { 2 } + 6 x + 9 }$

If the system has infinitely many solutions, write the solution set with x arbitrary. - 7x-6y=1 -14x+12y=1

Find the partial fraction decomposition for the rational expression. - $\frac { 4 x ^ { 3 } + 8 x ^ { 2 } + 5 x - 7 } { 2 x ^ { 2 } - x - 1 }$

Find the values of the variables for which the statement is true, if possible. - $\left[ \begin{array} { l l l } - 2 & b & 4 \end{array} \right] + \left[ \begin{array} { l l l } a & 8 & c \end{array} \right] = \left[ \begin{array} { l l l } 5 & - 1 & 4 \end{array} \right]$

Solve the system by substitution. - -2x=5y+19 -31=6y-3x

Review of Basic Concepts

Equations and Inequalities

Graphs and Functions

Polynomial and Rational Functions

Inverse, Exponential, and Logarithmic Functions

Trigonometric Functions

The Circular Functions and Their Graphs

Trigonometric Identities and Equations

Applications of Trigonometry

Analytic Geometry

Further Topics in Algebra

Filters

Exam 10: Systems and Matrices

Solve the problem. -Michael's bank contains only nickels, dimes, and quarters. There are 51 coins in all, valued at \$4.15. The number of nickels is 5 short of being three times the sum of the number of dimes and quarters. How many dimes are in the bank?

Solve the equation for x. - ∣−251x∣=−3\left| \begin{array} { r r } - 2 & 5 \\1 & x\end{array} \right| = - 3​−21​5x​​=−3

Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, give the solution with y arbitrary. - 2x+5y=-7 -6x-15y=21

Provide an appropriate response. -Suppose that AAA and BBB are two matrices such that A+B,A−BA + B , A - BA+B,A−B , and ABA BAB all exist. What can you conclude about the dimensions of A\mathrm { A }A and B\mathrm { B }B ?

Graph the solution set of the system of inequalities. - y\leq--6x-4 y\geq+6x+4

Provide an appropriate response. -Describe the characteristics of an augmented matrix in diagonal or reduced-row echelon form. 141)

Provide an appropriate response. -What is the value of ∣mnp000qrs∣\left| \begin{array} { l l l } \mathrm { m } & \mathrm { n } & \mathrm { p } \\0 & 0 & 0 \\\mathrm { q } & \mathrm { r } & \mathrm { s }\end{array} \right|​m0q​n0r​p0s​​ for any values of the variables?

Solve the system in terms of the arbitrary variable x. - x-6y+z=10 6x-y-z=18

Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, give the solution with y arbitrary. - 4x+3y=1 2x+4y=8

Write the augmented matrix for the system. Do not - 5x+5y+7z=23 -2x+9y+4z=6 2x+5y+2z=16

Find the partial fraction decomposition for the rational expression. - x2x2+6x+9\frac { x ^ { 2 } } { x ^ { 2 } + 6 x + 9 }x2+6x+9x2​

If the system has infinitely many solutions, write the solution set with x arbitrary. - 7x-6y=1 -14x+12y=1

Find the partial fraction decomposition for the rational expression. - 4x3+8x2+5x−72x2−x−1\frac { 4 x ^ { 3 } + 8 x ^ { 2 } + 5 x - 7 } { 2 x ^ { 2 } - x - 1 }2x2−x−14x3+8x2+5x−7​

Solve the system by substitution. - -2x=5y+19 -31=6y-3x

Review of Basic Concepts

Equations and Inequalities

Graphs and Functions

Polynomial and Rational Functions

Inverse, Exponential, and Logarithmic Functions

Trigonometric Functions

The Circular Functions and Their Graphs

Trigonometric Identities and Equations

Applications of Trigonometry

Analytic Geometry

Further Topics in Algebra

Filters

Solve the equation for x. - $\left| \begin{array} { r r } - 2 & 5 \\1 & x\end{array} \right| = - 3$

Provide an appropriate response. -Suppose that $A$ and $B$ are two matrices such that $A + B , A - B$ , and $A B$ all exist. What can you conclude about the dimensions of $\mathrm { A }$ and $\mathrm { B }$ ?

Graph the solution set of the system of inequalities. - y\leq--6x-4 y\geq+6x+4 $Graph the solution set of the system of inequalities. - \begin{array} { l } y \leq - x ^ { 2 } - 6 x - 4 \\ y \geq x ^ { 2 } + 6 x + 4 \end{array}$

Provide an appropriate response. -What is the value of $\left| \begin{array} { l l l } \mathrm { m } & \mathrm { n } & \mathrm { p } \\0 & 0 & 0 \\\mathrm { q } & \mathrm { r } & \mathrm { s }\end{array} \right|$ for any values of the variables?

Find the partial fraction decomposition for the rational expression. - $\frac { x ^ { 2 } } { x ^ { 2 } + 6 x + 9 }$

Find the partial fraction decomposition for the rational expression. - $\frac { 4 x ^ { 3 } + 8 x ^ { 2 } + 5 x - 7 } { 2 x ^ { 2 } - x - 1 }$