Exam 10: Systems and Matrices

Give all solutions of the nonlinear system of equations, including those with nonreal complex components. - $x ^ { 2 } + 3 x y + y ^ { 2 } = 4$ $x ^ { 2 } - 3 x y - y ^ { 2 } = 4$

Use Cramer's rule to solve the system of equations. If D = 0, use another method to determine the solution set. - 4x+3y+z=29 3x-2y-z=4 4x+y+3z=15

Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, give the solution with y arbitrary. - 7x+7y=-42 -4x-4y=24

Find the values of the variables for which the statement is true, if possible. - $\left[ \begin{array} { c c } x + 3 & y + 4 \\7 & - 8\end{array} \right] = \left[ \begin{array} { c c } 8 & - 5 \\7 & k\end{array} \right]$

If the system has infinitely many solutions, write the solution set with x arbitrary. - -= +=-

If the system has infinitely many solutions, write the solution set with x arbitrary. - 9x-y-10=0 -18x+2y+20=0

Give all solutions of the nonlinear system of equations, including those with nonreal complex components. - xy=11 2-=11

Use Cramer's rule to solve the system of equations. If D = 0, use another method to determine the solution set. - 8x-9y+4z=0 -4x+5y+5z=60 3x-7y-8z=-105

Provide an appropriate response. -Suppose that you are solving a system of three linear equations and have evaluated $D , D _ { X } , D _ { y }$ and $D _ { Z }$ . Under what condition does Cramer's rule not apply?

If the system has infinitely many solutions, write the solution set with x arbitrary. - ++=- +-= ++=-

The sizes of two matrices are given. Find the size of the product AB and the size of the product BA, if the given product can be calculated. - $\mathrm { A }$ is $2 \times 4 ; \mathrm { B }$ is $4 \times 2$

Graph the solution set of the system of inequalities. - y\geq- y\leqx+1 y\geq-5 x\leq-4

Find the values of the variables for which the statement is true, if possible. - $\left[ \begin{array} { c c c } - 4 & 8 & \mathrm { x } \\- 5 & \mathrm { y } & - 3\end{array} \right] = \left[ \begin{array} { r r r } \mathrm { m } & 8 & - 7 \\\mathrm { n } & 7 & \mathrm { p }\end{array} \right]$

Give all solutions of the nonlinear system of equations, including those with nonreal complex components. - 3+3=20 6+6=48

Perform the operation or operations when possible. - $\left[ \begin{array} { r r } - 1 & - 7 \\3 & 5 \\- 2 & 7\end{array} \right] + \left[ \begin{array} { r r } - 4 & 1 \\5 & 3 \\- 1 & - 7\end{array} \right]$

Decide whether or not the matrices are inverses of each other. - $\left[ \begin{array} { l l } 9 & 4 \\4 & 4\end{array} \right] \text { and } \left[ \begin{array} { r r } - .2 & .2 \\.2 & - .45\end{array} \right]$

Find the dimension of the matrix. - $\left[ \begin{array} { r r r } 6 & 4 & - 4 \\- 4 & - 8 & 5\end{array} \right]$

Find the indicated matrix. -Let $C = \left[ \begin{array} { r } 1 \\ - 3 \\ 2 \end{array} \right]$ and $D = \left[ \begin{array} { r } - 1 \\ 3 \\ 2 \end{array} \right]$ . Find $C - 2 D$ .

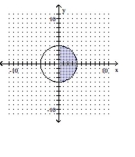
Determine the system of inequalities illustrated in the graph. Write inequalities in standard form. -

Find the matrix product when possible. -Mike's Bait Shop sells three types of lures: discount, normal, and professional. Location I sells 14 discount lures, 100 regular lures, and 30 professional lures each day. Location II sells 18 discount lures and Location III sells 60 discount lures each day. Daily sales of regular lures are 90 at Location II and 120 at Location III. At Location II, 37 expert lures are sold each day, and 40 expert lures are so each day at Location III. Write a $3 \times 3$ matrix that shows the sales figures for the three locations, with the rows representing the three locations. The incomes per lure for discount, normal, and professional lures are $\$ 5 , \$ 7$ , and $\$ 20$ , respectively. Write a $3 \times 1$ matrix displaying the incomes. Find a matrix product that gives the daily income at each of the three locations.