Exam 10: Systems and Matrices
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Provide an appropriate response.
-Suppose that you are solving a system of three linear equations by the Gauss-Jordan method and obtain the following augmented matrix.
What row transformation would you perform next?
(Multiple Choice)
4.8/5  (32)
(32)
A nonlinear system is given, along with the graphs of both equations in the system. Determine if the points of
intersection specified on the graph are solutions of the system by substituting directly into both equations.
- +=25 2y+x=5
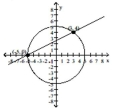
(Multiple Choice)
4.8/5  (40)
(40)
Use a graphing calculator to solve the nonlinear system. Give x- and y-coordinates to the nearest hundredth.
-A chair manufacturing company has two different factories. The profit function for Factory I when are manufactured and sold is as follows:
The profit function for Factory II when chairs are manufactured and sold is as follows:
For what number of chairs is the profit the same at both factories, and what is the profit?
(Multiple Choice)
4.7/5  (42)
(42)
Find the matrix product when possible.
-Le Boulangerie, a bakery, sells four main items: sweet rolls, bread, cakes, and pies. The amount of e. 44 ingredient (in cups, except for eggs) required for these items is given by matrix A.
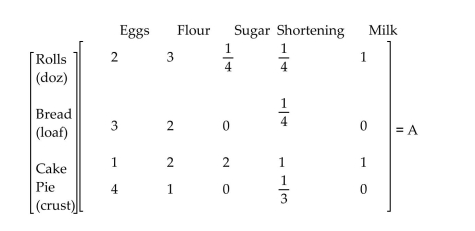 Suppose a day's orders consist of 20 dozen sweet rolls, 200 loaves of bread, 50 cakes, and 60 pies. Write the orders as a matrix and, using matrix multiplication, write as a matrix the amount of each ingredient needed to fill the day's orders.
Suppose a day's orders consist of 20 dozen sweet rolls, 200 loaves of bread, 50 cakes, and 60 pies. Write the orders as a matrix and, using matrix multiplication, write as a matrix the amount of each ingredient needed to fill the day's orders.
(Multiple Choice)
4.9/5  (35)
(35)
Solve the linear programming problem.
-An airline with two types of airplanes, and , has contracted with a tour group to provide transportation for a minimum of 400 first class, 900 tourist class, and 1500 economy class passengers. For a certain trip, airplane costs to operate and can accommodate 20 first class, 50 tourist class, and 110 economy class passengers. Airplane costs to operate and can accommodate 18 first class, 30 tourist class, and 44 economy class passengers. How many of each type of airplane should be used in order to minimize the operating cost?
(Multiple Choice)
4.7/5  (42)
(42)
Use a graphing calculator and the method of matrix inverses to Give five decimal places, if necessary.
-A bookstore is having a sale. All books included in the sale have a colored sticker on them to indicate the sale price. There are green stickers, red stickers, and orange stickers. Bob, Sue, and Fred each make purchases of books that are on sale. Each row of the table gives information about the numbers of book purchases and the total cost of the purchase (before taxes).
Person Green Red Orange Total Cost Bob 1 2 2 \ 29.04 Sue 1 3 2 \ 35.91 Fred 1 2 3 \ 34.21
Use this information to set up a matrix equation of the form , which can be solved to determ: the price for each type of sale book. Solve this matrix equation to find the price of a book with a red :
Use the fact that for .
(Multiple Choice)
4.8/5  (42)
(42)
Graph the solution set of the system of inequalities.
- y\geq y\leq8
(Multiple Choice)
5.0/5  (38)
(38)
Solve the problem.
-A company makes 3 types of cable. Cable A requires 3 black, 3 white, and 2 red wires. B requires 1 black, 2 white, and 1 red. requires 2 black, 1 white, and 2 red. The company used 100 black, 110 white and 80 red wires. How many of each type of cable were made?
(Multiple Choice)
4.7/5  (40)
(40)
Write the augmented matrix for the system. Do not
- 5x+5y+6z=61 7x+4y+3z=74 8x+7y-2z=84
(Multiple Choice)
4.8/5  (32)
(32)
Which method should be used to solve the system? Explain your answer, including a description of the first step.
-
(Multiple Choice)
4.8/5  (26)
(26)
If the system has infinitely many solutions, write the solution set with x arbitrary.
- 10x-y=5 -20x+2y=-10
(Multiple Choice)
4.7/5  (37)
(37)
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
-Which of the following properties do not hold for matrix multiplication?
(i) Associative property
(ii) Commutative property
(iii) Distributive property
(iv) Zero-factor property (If the product of two matrices is a zero matrix, then one of the factors must be a zero matrix.)
(Multiple Choice)
4.8/5  (42)
(42)
Graph the solution set of the system of inequalities.
- x-2y\leq2 x+y\leq0
(Multiple Choice)
4.9/5  (39)
(39)
Use a graphing calculator to Express solutions with approximations to the nearest thousandth.
- x-y=7 100x+y=9
(Multiple Choice)
4.7/5  (33)
(33)
Find the matrix product when possible.
-Momma's ice cream shop sells three types of ice cream: soft-serve, chunky, and nonfat. Location I sells 14 gal of soft-serve, 80 gal of chunky, and of nonfat ice cream each day. Location II sells 28 gal of soft-serve and Location III sells 60 gal of soft-serve each day. Daily sales of chunky ice cream are 90 gal at Location II and 120 gal at Location III. At Location II, 38 gal of nonfat are sold each day, and of nonfat are sold each day at Location III.
Write a matrix that shows the sales figures for the three locations, with the rows representing the three locations. The incomes per gallon for soft-serve, chunky, and nonfat ice cream are , and , respectively. Write a matrix displaying the incomes. Find a matrix product that gives the daily income at each of the three locations.
(Multiple Choice)
4.8/5  (33)
(33)
Write the system of equations associated with the augmented matrix. Do not solve.
-
(Multiple Choice)
4.8/5  (32)
(32)
Write the system of equations associated with the augmented matrix. Do not solve.
-
(Multiple Choice)
4.8/5  (45)
(45)
Use a graphing calculator to Express solutions with approximations to the nearest thousandth.
- 3x-2y-4z+1=0 9x-2y+8z-4=0 4y+4z-3=0
(Multiple Choice)
4.9/5  (34)
(34)
Showing 301 - 320 of 507
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)