Exam 10: Systems and Matrices
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Use a graphing calculator to Express solutions with approximations to the nearest thousandth.
- 0.4+=1 +0.8=1
(Multiple Choice)
4.8/5  (37)
(37)
Provide an appropriate response.
-You are graphing . You have drawn the graph of . What single point will allow you to determine the correct region?
(Multiple Choice)
4.9/5  (34)
(34)
Find the matrix product when possible.
-Mike's Bait Shop sells three types of lures: discount, normal, and professional. Location I sells 38 discount lures, 100 regular lures, and 30 professional lures each day. Location II sells 35 discount lures and Location III sells 60 discount lures each day. Daily sales of regular lures are 90 at Location II and 120 at Location III. At Location II, 35 expert lures are sold each day, and 40 expert lures are sold each day at Location III. Write a matrix that shows the sales figures for the three locations, with the rows representing the three locations.
(Multiple Choice)
4.9/5  (38)
(38)
Write the augmented matrix for the system. Do not
- 6x+5z-1=0 4y+8z-16=0 -2x+9y+7z-45=0
(Multiple Choice)
4.8/5  (39)
(39)
Solve the linear programming problem.
-An airline with two types of airplanes, and , has contracted with a tour group to provide transportation for a minimum of 400 first class, 750 tourist class, and 1500 economy class passengers. For a certain trip, airplane costs to operate and can accommodate 20 first class, 50 tourist class, and 110 economy class passengers. Airplane costs to operate and can accommodate 18 first class, 30 tourist class, and 44 economy class passengers. How many of each type of airplane should be used in order to minimize the operating cost?
(Multiple Choice)
4.8/5  (38)
(38)
If the system has infinitely many solutions, write the solution set with x arbitrary.
- += -=-
(Multiple Choice)
4.7/5  (33)
(33)
Graph the solution set of the system of inequalities.
- y-x\leq5 x+y\geq3 y-3x\geq-1
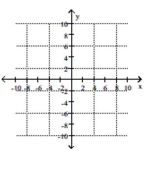
(Multiple Choice)
4.7/5  (40)
(40)
Find the partial fraction decomposition for the rational expression.
-
(Multiple Choice)
4.8/5  (31)
(31)
Solve the problem.
-Carole's car averages in city driving and in highway driving. If she drove a total of on of gas, how many of the gallons were used for city driving?
(Multiple Choice)
4.8/5  (27)
(27)
Solve the system by using the inverse of the coefficient matrix.
- -5x+3y=8 3x-6y=-30
(Multiple Choice)
4.7/5  (40)
(40)
A nonlinear system is given, along with the graphs of both equations in the system. Determine if the points of
intersection specified on the graph are solutions of the system by substituting directly into both equations.
- +=52 2y+3x=0
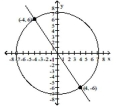
(Multiple Choice)
4.7/5  (40)
(40)
The following graph shows the populations of the metropolitan areas of City X and City Y over six years. 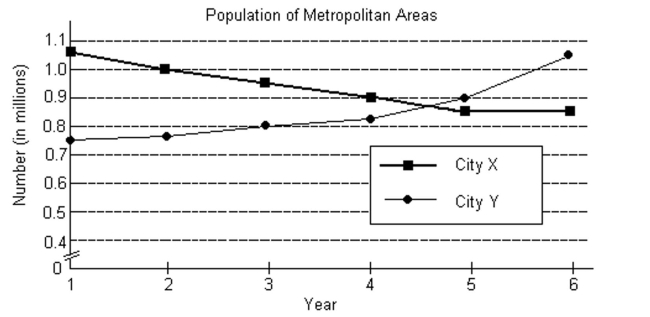 -In what years was the population of the City X metropolitan area less than that of the City Y metropolitan area?
-In what years was the population of the City X metropolitan area less than that of the City Y metropolitan area?
(Multiple Choice)
4.7/5  (34)
(34)
Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, let the last
variable be the arbitrary variable.
- 3x-7y-z =-28 x-9y+9z =-28 3x+y+z =34
(Multiple Choice)
4.9/5  (43)
(43)
Which method should be used to solve the system? Explain your answer, including a description of the first step.
-
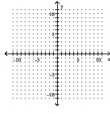
(Multiple Choice)
4.9/5  (39)
(39)
The graph shows the region of feasible solutions. Find the maximum or minimum value, as specified, of the objective
function.
-
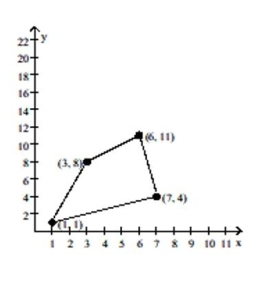
(Multiple Choice)
4.8/5  (37)
(37)
Use the given row transformation to change the matrix as indicated.
- times row 1 added to row 2
(Multiple Choice)
4.8/5  (30)
(30)
Use a graphing calculator to solve the nonlinear system. Give x- and y-coordinates to the nearest hundredth.
- +=7 y=
(Multiple Choice)
4.8/5  (44)
(44)
Showing 281 - 300 of 507
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)