Exam 10: Systems and Matrices
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
If the system has infinitely many solutions, write the solution set with x arbitrary.
- 3x+2y+z=4 2x-3y-z=5 5x+12y+5z=2
(Multiple Choice)
4.9/5  (37)
(37)
20Solve the system using a graphing calculator capable of performing row operations. Give solutions with values correct to
the nearest thousandth.
- 0.6x+4.9y-z=7 x-18y+10z=-1 3x+y-4.9z=
(Multiple Choice)
4.9/5  (37)
(37)
Solve the system by using the inverse of the coefficient matrix.
- x+3y=-8 -14x-4y=-2
(Multiple Choice)
4.9/5  (47)
(47)
Use the shading capabilities of your graphing calculator to graph the inequality or system of inequalities.
- y\geq|x+6| y\leq3
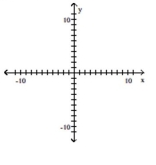
(Multiple Choice)
4.9/5  (38)
(38)
Solve the linear programming problem.
-The Acme Class Ring Company designs and sells two types of rings: the VIP and the SST. They can produce up to 24 rings each day using up to 60 total man-hours of labor. It takes 3 man-hours to make one VIP ring and 2 man-hours to make one SST ring. How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
(Multiple Choice)
4.8/5  (42)
(42)
Solve the system by using the inverse of the coefficient matrix.
- 5x+4y=8 6x-3y=33
(Multiple Choice)
4.9/5  (36)
(36)
Use a graphing calculator and the method of matrix inverses to Give five decimal places, if necessary.
- (2)x+(3)y+(5)z=4 (3)x+(8)y+(10)z=11 (23)x+(7)y+(4)z=15
(Multiple Choice)
4.7/5  (31)
(31)
Find the values of the variables for which the statement is true, if possible.
-
(Multiple Choice)
4.8/5  (23)
(23)
Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, let the last
variable be the arbitrary variable.
- -3x-y-8z=-64 4x+9z=74 8y+z=14
(Multiple Choice)
4.8/5  (32)
(32)
Solve the system by using the inverse of the coefficient matrix.
- 2x+8y+6z=20 4x+2y-2z=-2
(Multiple Choice)
4.8/5  (39)
(39)
Find the values of the variables for which the statement is true, if possible.
-
(Multiple Choice)
4.9/5  (39)
(39)
A nonlinear system is given, along with the graphs of both equations in the system. Determine if the points of
intersection specified on the graph are solutions of the system by substituting directly into both equations.
- =y-1 y=3x+11
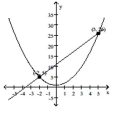
(Multiple Choice)
4.8/5  (27)
(27)
Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, give the
solution with y arbitrary.
- 5x-2y-10=0 10x+y-25=0
(Multiple Choice)
4.8/5  (30)
(30)
If the system has infinitely many solutions, write the solution set with x arbitrary.
- +=3 -=-3
(Multiple Choice)
4.8/5  (33)
(33)
Solve the system for x and y using Cramer's rule. Assume a and b are nonzero constants.
-
(Multiple Choice)
4.9/5  (39)
(39)
The sizes of two matrices are given. Find the size of the product AB and the size of the product BA, if the given product
can be calculated.
-A is ; B is
(Multiple Choice)
5.0/5  (40)
(40)
Showing 481 - 500 of 507
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)