Exam 10: Systems and Matrices
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Provide an appropriate response.
-Let and
Does the matrix have an inverse?
(Multiple Choice)
4.7/5  (36)
(36)
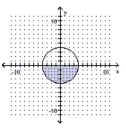
Determine the system of inequalities illustrated in the graph. Write inequalities in standard form.
-
(Multiple Choice)
4.7/5  (32)
(32)
Write the augmented matrix for the system. Do not
- 9x+6y=-3 5x+2y=1
(Multiple Choice)
4.8/5  (35)
(35)
Solve the system to find
-Linear systems occur in the design of roof trusses for new homes and buildings. The simplest type 223) of roof truss is a triangle. The truss shown in the figure is used to frame roofs of small buildings. If
A force of 116 pounds is applied at the peak of the truss, then the forces or weight exerted parallel to each rafter of the truss are determined by the following linear system of equations. 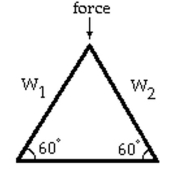 + =116 -=0
+ =116 -=0
(Multiple Choice)
4.9/5  (35)
(35)
Use a graphing calcula tor to find the inverse of the matrix. Give five decimal places, if necessary.
-
(Multiple Choice)
4.8/5  (35)
(35)
Give all solutions of the nonlinear system of equations, including those with nonreal complex components.
- +=80 -=48
(Multiple Choice)
4.8/5  (36)
(36)
Use a graphing calculator to Express solutions with approximations to the nearest thousandth.
- 2x-y-5z=-14 -2x+4y+4z=16 -8x-4y+z=-36
(Multiple Choice)
5.0/5  (32)
(32)
Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, give the
solution with y arbitrary.
- 3x+y=10 9x+4y=25
(Multiple Choice)
4.9/5  (40)
(40)
Solve the system to find
-Linear systems occur in the design of roof trusses for new homes and buildings. The simplest type of roof truss is a triangle. The truss shown in the figure is used to frame roofs of small buildings. If
A 172-pound force is applied at the peak of the truss, then the forces or weights W exerted
Parallel to each rafter of the truss are determined by the following linear system of equations. 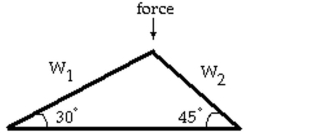 +=344 -=0
+=344 -=0
(Multiple Choice)
4.8/5  (28)
(28)
Give all solutions of the nonlinear system of equations, including those with nonreal complex components.
- y=|x| 4x-y=-20
(Multiple Choice)
4.8/5  (40)
(40)
Use a graphing calculator to Express solutions with approximations to the nearest thousandth.
- 1.2x+y=-8 -4.5x-y=10
(Multiple Choice)
4.8/5  (29)
(29)
The sizes of two matrices are given. Find the size of the product AB and the size of the product BA, if the given product
can be calculated.
-A is ; B is .
(Multiple Choice)
4.8/5  (39)
(39)
Which method should be used to solve the system? Explain your answer, including a description of the first step.
-
(Multiple Choice)
4.8/5  (34)
(34)
Provide an appropriate response.
-Fill in the blank to complete the statement. Each number in a matrix is called of the matrix.
(Multiple Choice)
4.9/5  (32)
(32)
Showing 181 - 200 of 507
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)