Exam 5: Inverse, Exponential, and Logarithmic Functions
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Find the domain and range of the inverse of the given function.
-
(Multiple Choice)
4.9/5  (30)
(30)
Find the future value.
-$59,878 invested for 3 years at 5% compounded semiannually 159)
(Multiple Choice)
4.7/5  (30)
(30)
Choose the one alternative that best completes the statement or answers the question.
-Suppose the consumption of electricity grows at per year, compounded continuously. Find the number of years before the use of electricity has tripled. Round the answer to the nearest hundredth.
(Multiple Choice)
4.9/5  (46)
(46)
Solve the equation and express the solution in exact form.
-
(Multiple Choice)
4.8/5  (36)
(36)
Write the expression as a single logarithm with coefficient 1. Assume all variables represent positive real numbers with
-
(Multiple Choice)
4.9/5  (36)
(36)
Choose the one alternative that best completes the statement or answers the question.
-A population is increasing according to the exponential function defined by , where is in millions and is the number of years. Which of the following should be done in order to answer the question "How large will the population be in 4 years?"
(Multiple Choice)
4.7/5  (36)
(36)
Use properties of logarithms to evaluate the expression.
-If , find
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-Given that , find and give the domain and range of
(Multiple Choice)
4.7/5  (32)
(32)
The graph of a function f is given. Use the graph to find the indicated value.
-
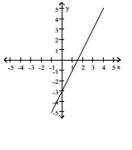
(Multiple Choice)
4.7/5  (29)
(29)
Solve the problem.
-The population of a particular city is increasing at a rate proportional to its size. It follows the function where is a constant and is the time in years. If the current population is 18,000 , in how many years is the population expected to be 45,000 ? Round to the nearest year.
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-How long must $4700 be in a bank at 6% compounded annually to become $7067.06? (Round to the nearest year.)
(Multiple Choice)
5.0/5  (29)
(29)
Provide an appropriate response.
-Give an equation of the form to define the exponential function whose graph contains the point . Assume that .
(Multiple Choice)
4.9/5  (33)
(33)
Write the word or phrase that best completes each statement or answers the question.
-
(Essay)
4.7/5  (37)
(37)
Use the definition of inverses to determine whether f and g are inverses.
-
(Multiple Choice)
4.8/5  (36)
(36)
The graph of a function f is given. Use the graph to find the indicated value.
-
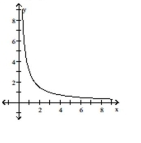
(Multiple Choice)
4.8/5  (26)
(26)
Showing 381 - 400 of 472
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)