Exam 5: Inverse, Exponential, and Logarithmic Functions
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Use properties of logarithms to evaluate the expression.
-If , find
(Multiple Choice)
4.9/5  (40)
(40)
Determine whether the statement is true or false.
-The function f b is a one-to-one function for all values of m and b.
(True/False)
4.8/5  (38)
(38)
Solve the problem.
-An earthquake was recorded with an intensity which was 50,119 times more powerful than a reference level earthquake, or 50,119 · I0. What is the magnitude of this earthquake on the Richter
Scale (rounded to the nearest tenth)? Intensity on the Richter scale is
(Multiple Choice)
5.0/5  (40)
(40)
Solve the problem.
-Given that , find and give the domain and range of
(Multiple Choice)
4.8/5  (33)
(33)
Use the properties of logarithms to rewrite the expression. Simplify the result if possible. Assume all variables represent
positive real numbers.
-
(Multiple Choice)
4.8/5  (42)
(42)
Solve the following graphically. If necessary, round answers to the nearest thousandth.
-
(Multiple Choice)
4.9/5  (29)
(29)
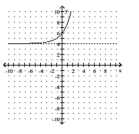
Write an equation for the graph given. The graph represents an exponential function f with base 2 or 3, translated and/or
reflected.
-
(Multiple Choice)
4.9/5  (36)
(36)
Write the word or phrase that best completes each statement or answers the question.
-Explain how the graph of an be obtained from the graph of y
(Short Answer)
4.8/5  (40)
(40)
Provide an appropriate response.
-Give an equation of the form to define the exponential function whose graph contains the point . Assume that .
(Multiple Choice)
4.8/5  (32)
(32)
Solve the following graphically. If necessary, round answers to the nearest thousandth.
-
(Multiple Choice)
4.9/5  (25)
(25)
The graph of a function f is given. Use the graph to find the indicated value.
-Let f(x) compute the time in hours to travel x miles at 60 miles per hour. What is the interpretation of
(Multiple Choice)
4.8/5  (31)
(31)
Solve the equation and express the solution in exact form.
-
(Multiple Choice)
4.9/5  (29)
(29)
Solve the equation and express the solution in exact form.
-
(Multiple Choice)
4.8/5  (40)
(40)
Showing 121 - 140 of 472
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)