Exam 5: Inverse, Exponential, and Logarithmic Functions
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Solve the problem.
-Suppose models salinity of ocean water to depths of 1000 meters at a certain latitude. is the depth in meters and is in grams of salt per kilogram of seawater. Approximate the depth (to the nearest tenth of a meter) where the salinity equals 36 .
(Multiple Choice)
5.0/5  (40)
(40)
Graph the exponential function using transformations where appropriate.
-
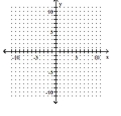
(Multiple Choice)
4.8/5  (26)
(26)
Write the expression as a single logarithm with coefficient 1. Assume all variables represent positive real numbers with
-
(Multiple Choice)
4.8/5  (34)
(34)
Use a graphing calculator to estimate the solution set of the equation. Round to the nearest hundredth.
-
(Multiple Choice)
4.7/5  (40)
(40)
Graph the exponential function using transformations where appropriate.
-
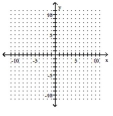
(Multiple Choice)
4.7/5  (36)
(36)
If the function is one-to-one, find its inverse. If not, write "not one-to-one."
-
(Multiple Choice)
4.9/5  (33)
(33)
Decide whether the given functions are inverses.
- =\{(3,6),(3,3),(0,8)\} g=\{(3,3),(8,0),(6,6)\}
(Multiple Choice)
4.7/5  (28)
(28)
Find the function value. If the result is irrational, round your answer to the nearest thousandth.
-Let . Find .
(Multiple Choice)
4.9/5  (34)
(34)
Choose the one alternative that best completes the statement or answers the question.
-An economist predicts that the buying power of a dollar years from now will decrease according to the formula . How much will today's dollar be worth in 2 years? Round the answer to the nearest cent.
(Multiple Choice)
4.9/5  (47)
(47)
Find the value. Give an approximation to four decimal places.
-
(Multiple Choice)
4.7/5  (40)
(40)
Find the domain and range of the inverse of the given function.
-
(Multiple Choice)
4.8/5  (27)
(27)
Find the present value of the future value.
- The half-life of Cesium 134m is 3.0 hours. If the formula gives the percent (as a decimal) remaining after time t (in hours), sketch P versus t. 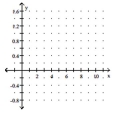
(Multiple Choice)
4.9/5  (27)
(27)
Write the expression as a single logarithm with coefficient 1. Assume all variables represent positive real numbers with
-
(Multiple Choice)
4.8/5  (29)
(29)
Use the properties of logarithms to rewrite the expression. Simplify the result if possible. Assume all variables represent
positive real numbers.
-
(Multiple Choice)
4.8/5  (27)
(27)
Choose the one alternative that best completes the statement or answers the question.
-Use the formula , where the loudness of a sound in decibels is determined by , the number of watt produced by the soundwave, and watt . A certain noise produces of power. What is the decibel level of this noise? (Round to the nearest unit.)
(Multiple Choice)
4.8/5  (41)
(41)
Round your answer to the nearest tenth, when appropriate. Use the formula needed.
-Find the if .
(Multiple Choice)
4.9/5  (43)
(43)
Explain how the graph of can be obtained from the graph o
-Give a definition for the following term: Logarithmic function .
(Essay)
4.8/5  (26)
(26)
Showing 161 - 180 of 472
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)