Exam 5: Inverse, Exponential, and Logarithmic Functions
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Choose the one alternative that best completes the statement or answers the question.
-A sample of 650 grams of radioactive substance decays according to the function , where is the time in years. How much of the substance will be left in the sample after 20 years? Round your answer to the nearest whole gram.
(Multiple Choice)
4.9/5  (38)
(38)
Use a graphing calculator to estimate the solution set of the equation. Round to the nearest hundredth.
-
(Multiple Choice)
4.9/5  (37)
(37)
For the function as defined that is one-to-one, graph f and on the same axes.
-
(Multiple Choice)
4.8/5  (19)
(19)
Use a graphing calculator to estimate the solution set of the equation. Round to the nearest hundredth.
-
(Multiple Choice)
4.9/5  (29)
(29)
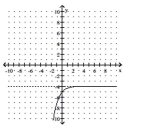
Write an equation for the graph given. The graph represents an exponential function f with base 2 or 3, translated and/or
reflected.
-
(Multiple Choice)
4.9/5  (25)
(25)
Choose the one alternative that best completes the statement or answers the question.
-A population is increasing according to the exponential function defined by y , where y is in millions and x is the number of years. Which of the following should be done in order to answer
The question "When will the population reach 4 million?"
(Multiple Choice)
4.8/5  (33)
(33)
Solve the equation and express the solution in exact form.
-
(Multiple Choice)
4.7/5  (34)
(34)
Choose the one alternative that best completes the statement or answers the question.
-Suppose that can be used to calculate the number of years for percent of a population of 680 web-footed sparrows to die. Approximate the percentage (to the nearest whole per cent) of web-footed sparrows that died after 3 years.
(Multiple Choice)
4.9/5  (39)
(39)
Graph the exponential function using transformations where appropriate.
-
(Multiple Choice)
4.7/5  (32)
(32)
Write the word or phrase that best completes each statement or answers the question.
-Explain the error in the following:
(Essay)
4.9/5  (26)
(26)
Solve the problem.
-An earthquake had an intensity times more powerful than a reference level earthquake, or . What was the magnitude of this earthquake on the Richter scale? .
(Multiple Choice)
4.7/5  (34)
(34)
Choose the one alternative that best completes the statement or answers the question.
-A certain radioactive isotope has a half-life of approximately 1250 years. How many years to the nearest year would be required for a given amount of this isotope to decay to of that amount?
(Multiple Choice)
4.8/5  (32)
(32)
Showing 41 - 60 of 472
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)