Exam 8: Polar Coordinates; Vectors
Exam 1: Functions and Their Graphs297 Questions
Exam 2: Linear and Quadratic Functions302 Questions
Exam 3: Polynomial and Rational Functions354 Questions
Exam 4: Exponential and Logarithmic Functions517 Questions
Exam 5: Trigonometric Functions354 Questions
Exam 6: Analytic Trigonometry342 Questions
Exam 7: Applications of Trigonometric Functions105 Questions
Exam 8: Polar Coordinates; Vectors253 Questions
Exam 9: Analytic Geometry200 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability115 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Foundations: a Prelude to Functions234 Questions
Exam 15: Graphing Utilities29 Questions
Select questions type
Find the angle between v and w. Round to one decimal place, if necessary.
-
(Multiple Choice)
4.7/5  (36)
(36)
Use the given vectors to find the indicated expression.
-
Find .
(Multiple Choice)
4.7/5  (38)
(38)
Transform the polar equation to an equation in rectangular coordinates. Then identify and graph the equation.
-
(Multiple Choice)
5.0/5  (39)
(39)
Decompose v into two vectors v1 and v2, where v1 is parallel to w and v2 is orthogonal to w.
-
(Multiple Choice)
4.8/5  (36)
(36)
Choose the one alternative that best completes the statement or answers the question.
The polar coordinates of a point are given. Find the rectangular coordinates of the point.
- Round the rectangular coordinates to two decimal places.
(Multiple Choice)
4.9/5  (26)
(26)
Choose the one alternative that best completes the statement or answers the question.
Find the direction angles of the vector. Round to the nearest degree, if necessary.
-
(Multiple Choice)
4.8/5  (35)
(35)
The rectangular coordinates of a point are given. Find polar coordinates for the point.
-
(Multiple Choice)
4.8/5  (26)
(26)
Use the vectors in the figure below to graph the following vector. 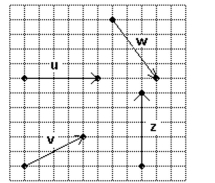 -
-
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-Find a vector v whose magnitude is 26 and whose component in the i direction is twice the component in the j direction.
(Multiple Choice)
4.9/5  (40)
(40)
Write the word or phrase that best completes each statement or answers the question.
Solve the problem.
-An airplane has an air speed of 550 miles per hour bearing N30°W. The wind velocity is 50 kilometers per hour
in the direction N30°E. Find the resultant vector (with exact components) representing the path of the plane
relative to the ground. To the nearest tenth, what is the ground speed of the plane? What is its direction?
(Essay)
4.9/5  (35)
(35)
Showing 41 - 60 of 253
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)