Exam 10: Conic Sections and Analytic Geometry
Exam 1: Equations and Inequalities425 Questions
Exam 2: Functions and Graphs359 Questions
Exam 3: Polynomial and Rational Functions532 Questions
Exam 4: Exponential and Logarithmic Functions270 Questions
Exam 5: Trigonometric Functions386 Questions
Exam 6: Analytic Trigonometry226 Questions
Exam 7: Additional Topics in Trigonometry264 Questions
Exam 8: Systems of Equations and Inequalities288 Questions
Exam 9: Matrices and Determinants152 Questions
Exam 10: Conic Sections and Analytic Geometry228 Questions
Exam 11: Sequences, Induction, and Probability304 Questions
Exam 12: Prerequisites: Fundamental Concepts of Algebra409 Questions
Select questions type
Convert the equation to the standard form for an ellipse by completing the square on x and y.
-
(Multiple Choice)
4.8/5  (30)
(30)
Find the solution set for the system by graphing both of the system's equations in the same rectangular coordinate system and finding points of intersection.
- 4+=4 -4=4
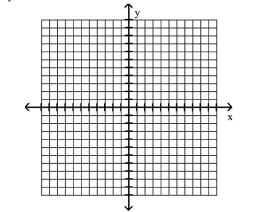
(Multiple Choice)
4.8/5  (36)
(36)
Understand the Advantages of Parametric Representations
-A baseball pitcher throws a baseball with an initial velocity of 126 feet per second at an angle of to the horizontal. The ball leaves the pitcher's hand at a height of 5 feet. Find parametric equations that describe the motion of the ball as a function of time. How long is the ball in the air? When is the ball at its maximum height? What is the maximum height of the ball?
(Multiple Choice)
4.7/5  (40)
(40)
Use the center, vertices, and asymptotes to graph the hyperbola.
-
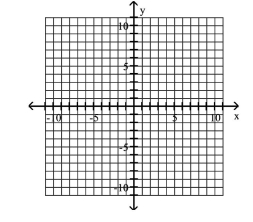
(Multiple Choice)
4.9/5  (35)
(35)
Parametric Equations
1 Use Point Plotting to Graph Plane Curves Described by Parametric Equations
-
(Multiple Choice)
4.8/5  (42)
(42)
The Parabola
1 Graph Parabolas with Vertices at the Origin
-
(Multiple Choice)
4.8/5  (28)
(28)
Graph the ellipse and locate the foci.
-
Round to the nearest tenth if necessary.
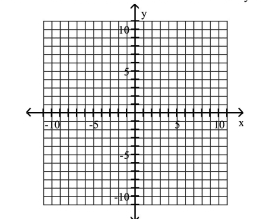
(Multiple Choice)
4.8/5  (37)
(37)
Find Parametric Equations for Functions
-Circle: Center: ; Radius: 2
(Multiple Choice)
4.9/5  (30)
(30)
Use the center, vertices, and asymptotes to graph the hyperbola.
-
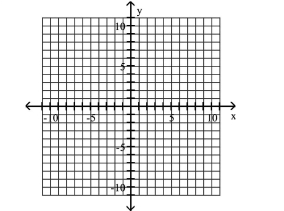
(Multiple Choice)
4.9/5  (40)
(40)
Showing 181 - 200 of 228
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)