Exam 10: Conic Sections and Analytic Geometry
Exam 1: Equations and Inequalities425 Questions
Exam 2: Functions and Graphs359 Questions
Exam 3: Polynomial and Rational Functions532 Questions
Exam 4: Exponential and Logarithmic Functions270 Questions
Exam 5: Trigonometric Functions386 Questions
Exam 6: Analytic Trigonometry226 Questions
Exam 7: Additional Topics in Trigonometry264 Questions
Exam 8: Systems of Equations and Inequalities288 Questions
Exam 9: Matrices and Determinants152 Questions
Exam 10: Conic Sections and Analytic Geometry228 Questions
Exam 11: Sequences, Induction, and Probability304 Questions
Exam 12: Prerequisites: Fundamental Concepts of Algebra409 Questions
Select questions type
Solve Apps: Conic Sections in Polar Coordinates
-Halley's comet has an elliptical orbit with the sun at one focus. Its orbit shown below is given approximately by . In the formula, is measured in astronomical units. (One astronomical unit is the average distance from Earth to the sun, approximately 93 million miles.)
Find the distance from Halley's comet to the sun at its shortest distance from the sun. Round to the nearest hundredth of an astronomical unit and the nearest million miles.
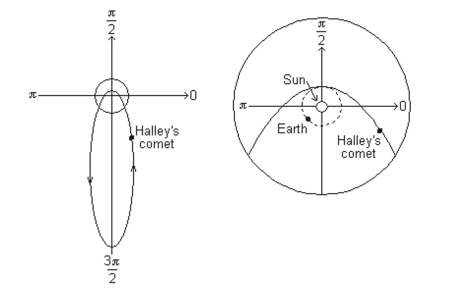
(Multiple Choice)
4.8/5  (26)
(26)
Use the center, vertices, and asymptotes to graph the hyperbola.
-
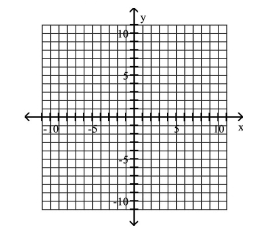
(Multiple Choice)
4.9/5  (31)
(31)
Solve Applied Problems Involving Parabolas
-A bridge is built in the shape of a parabolic arch. The bridge arch has a span of 184 feet and a maximum height of 40 feet. Find the height of the arch at 15 feet from its center.
(Multiple Choice)
4.8/5  (30)
(30)
Use point plotting to graph the plane curve described by the given parametric equations.
-
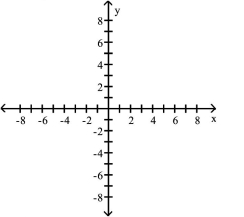
(Multiple Choice)
4.9/5  (38)
(38)
Rotation of Axes
1 Identify Conics Without Completing the Square
-
(Multiple Choice)
4.9/5  (33)
(33)
Write the appropriate rotation formulas so that in a rotated system the equation has no x'y'-term.
-
(Multiple Choice)
4.7/5  (38)
(38)
Write Equations of Hyperbolas in Standard Form
-Center: ; Focus: ; Vertex:
(Multiple Choice)
4.8/5  (45)
(45)
Showing 21 - 40 of 228
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)