Exam 10: Conic Sections and Analytic Geometry
Exam 1: Equations and Inequalities425 Questions
Exam 2: Functions and Graphs359 Questions
Exam 3: Polynomial and Rational Functions532 Questions
Exam 4: Exponential and Logarithmic Functions270 Questions
Exam 5: Trigonometric Functions386 Questions
Exam 6: Analytic Trigonometry226 Questions
Exam 7: Additional Topics in Trigonometry264 Questions
Exam 8: Systems of Equations and Inequalities288 Questions
Exam 9: Matrices and Determinants152 Questions
Exam 10: Conic Sections and Analytic Geometry228 Questions
Exam 11: Sequences, Induction, and Probability304 Questions
Exam 12: Prerequisites: Fundamental Concepts of Algebra409 Questions
Select questions type
Find two sets of parametric equations for the given rectangular equation.
-
(Multiple Choice)
4.8/5  (40)
(40)
Solve Applied Problems Involving Hyperbolas
-A satellite following the hyperbolic path shown in the picture turns rapidly at and then moves closer and closer to the line as it gets farther from the tracking station at the origin. Find the equation that describes the path of the satellite if the center of the hyperbola is at .
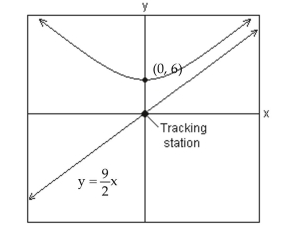
(Multiple Choice)
4.8/5  (30)
(30)
Solve Applied Problems Involving Parabolas
-A satellite dish is in the shape of a parabolic surface. Signals coming from a satellite strike the surface of the dish and are reflected to the focus, where the receiver is located. The satellite dish shown has a diameter of 6 feet and a depth of 6 feet. The parabola is positioned in a rectangular coordinate system with its vertex at the origin. The receiver should be placed at the focus . The value of is given by the equation . How far from the base of the dish should the receiver be placed?.
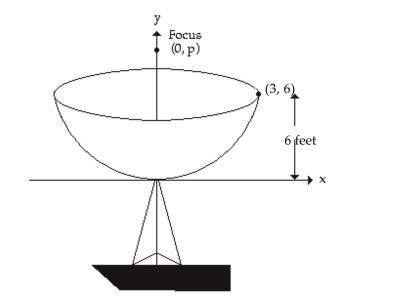
(Multiple Choice)
4.7/5  (40)
(40)
Convert the equation to the standard form for a hyperbola by completing the square on x and y.
-
(Multiple Choice)
4.7/5  (34)
(34)
Find the standard form of the equation of the ellipse satisfying the given conditions.
-Endpoints of major axis: and ; endpoints of minor axis: and
(Multiple Choice)
5.0/5  (27)
(27)
Solve Applied Problems Involving Hyperbolas
-Two recording devices are set 3200 feet apart, with the device at point A to the west of the device at point B. At a point on a line between the devices, 400 feet from point B, a small amount of explosive is detonated. The recording devices record the time the sound reaches each one. How far directly north of site B should a second explosion be done so that the measured time difference recorded by the devices is the same as that for the first detonation?
(Multiple Choice)
4.9/5  (35)
(35)
The Parabola
1 Graph Parabolas with Vertices at the Origin
-
(Multiple Choice)
4.9/5  (40)
(40)
Write the appropriate rotation formulas so that in a rotated system the equation has no x'y'-term.
-
(Multiple Choice)
4.8/5  (41)
(41)
Additional Concepts
- Find the equations of the asymptotes.
(Multiple Choice)
4.8/5  (34)
(34)
Find the standard form of the equation of the ellipse satisfying the given conditions.
-Major axis vertical with length length of minor axis center
(Multiple Choice)
4.7/5  (33)
(33)
Use point plotting to graph the plane curve described by the given parametric equations.
-
(Multiple Choice)
4.8/5  (23)
(23)
Write the word or phrase that best completes each statement or answers the question. The parametric equations of four curves are given. Graph each of them, indicating the orientation.
- :x=7t,y=7-7t;\leqt\leq :x=t,y=;\leqt\leq :x=-8,y=t-3;-4\leqt\leq4 :x=t-5,y=t+2;-4\leqt\leq7
(Essay)
4.8/5  (31)
(31)
Showing 81 - 100 of 228
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)