Exam 10: Conic Sections and Analytic Geometry
Exam 1: Equations and Inequalities425 Questions
Exam 2: Functions and Graphs359 Questions
Exam 3: Polynomial and Rational Functions532 Questions
Exam 4: Exponential and Logarithmic Functions270 Questions
Exam 5: Trigonometric Functions386 Questions
Exam 6: Analytic Trigonometry226 Questions
Exam 7: Additional Topics in Trigonometry264 Questions
Exam 8: Systems of Equations and Inequalities288 Questions
Exam 9: Matrices and Determinants152 Questions
Exam 10: Conic Sections and Analytic Geometry228 Questions
Exam 11: Sequences, Induction, and Probability304 Questions
Exam 12: Prerequisites: Fundamental Concepts of Algebra409 Questions
Select questions type
Find Parametric Equations for Functions
-Ellipse: Center: ; Vertices: 6 units above and below the center; Endpoints of Minor Axis: 4 units left and right of the center.
(Multiple Choice)
4.9/5  (38)
(38)
Convert the equation to the standard form for a parabola by completing the square on x or y as appropriate.
-
(Multiple Choice)
4.8/5  (41)
(41)
Find Parametric Equations for Functions
-Hyperbola: Vertices: ; Vertices: ; Foci: and
(Multiple Choice)
4.8/5  (37)
(37)
Write the appropriate rotation formulas so that in a rotated system the equation has no x'y'-term.
-
(Multiple Choice)
4.9/5  (34)
(34)
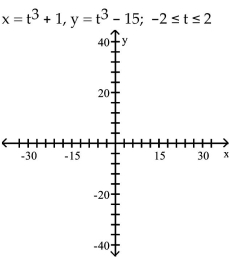
Use point plotting to graph the plane curve described by the given parametric equations.
-
(Multiple Choice)
4.8/5  (30)
(30)
Write Equations of Parabolas in Standard Form
-Focus: ; Directrix:
(Multiple Choice)
4.9/5  (33)
(33)
Write Equations of Hyperbolas in Standard Form
-Foci: ; vertices:
(Multiple Choice)
4.9/5  (34)
(34)
Conic Sections in Polar Coordinates
1 Define Conics in Terms of a Focus and a Directrix
-
(Multiple Choice)
4.9/5  (30)
(30)
Find the standard form of the equation of the ellipse satisfying the given conditions.
-Foci: ; vertices:
(Multiple Choice)
4.8/5  (31)
(31)
Conic Sections in Polar Coordinates
1 Define Conics in Terms of a Focus and a Directrix
-
(Multiple Choice)
4.9/5  (32)
(32)
Showing 201 - 220 of 228
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)