Exam 10: Conic Sections and Analytic Geometry
Exam 1: Equations and Inequalities425 Questions
Exam 2: Functions and Graphs359 Questions
Exam 3: Polynomial and Rational Functions532 Questions
Exam 4: Exponential and Logarithmic Functions270 Questions
Exam 5: Trigonometric Functions386 Questions
Exam 6: Analytic Trigonometry226 Questions
Exam 7: Additional Topics in Trigonometry264 Questions
Exam 8: Systems of Equations and Inequalities288 Questions
Exam 9: Matrices and Determinants152 Questions
Exam 10: Conic Sections and Analytic Geometry228 Questions
Exam 11: Sequences, Induction, and Probability304 Questions
Exam 12: Prerequisites: Fundamental Concepts of Algebra409 Questions
Select questions type
Write Equations of Parabolas in Standard Form
-Vertex: ; Focus:
(Multiple Choice)
4.9/5  (31)
(31)
Understand the Advantages of Parametric Representations
-Ron throws a ball straight up with an initial velocity of 40 feet per second from a height of 5 feet. Find parametric equations that describe the motion of the ball as a function of time. How long is the ball in the air? When is the ball at its maximum height? What is the maximum height of the ball?
(Multiple Choice)
4.7/5  (31)
(31)
Find the solution set for the system by graphing both of the system's equations in the same rectangular coordinate system and finding points of intersection.
- (y-6 =x+36 y =-x
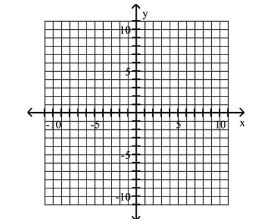
(Multiple Choice)
4.8/5  (35)
(35)
Parametric Equations
1 Use Point Plotting to Graph Plane Curves Described by Parametric Equations
-
(Multiple Choice)
4.8/5  (30)
(30)
Conic Sections in Polar Coordinates
1 Define Conics in Terms of a Focus and a Directrix
-
(Multiple Choice)
5.0/5  (40)
(40)
Write Equations of Parabolas in Standard Form
-Vertex: ; Focus:
(Multiple Choice)
4.8/5  (37)
(37)
Find the standard form of the equation of the ellipse satisfying the given conditions.
-Foci: -intercepts: and 8
(Multiple Choice)
4.8/5  (37)
(37)
Use point plotting to graph the plane curve described by the given parametric equations.
-
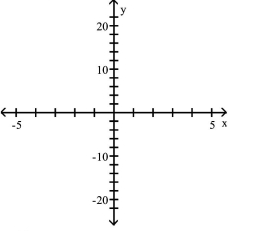
(Multiple Choice)
4.9/5  (31)
(31)
Solve Applied Problems Involving Parabolas
-An experimental model for a suspension bridge is built. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second tower. The towers stand 80 inches apart. At a point between the towers and 20 inches along the road from the base of one tower, the cable is 4 inches above the roadway. Find the height of the towers.
(Multiple Choice)
4.7/5  (39)
(39)
Showing 41 - 60 of 228
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)