Exam 14: Introduction to Multiple

14-30 Introduction to Multiple Regression 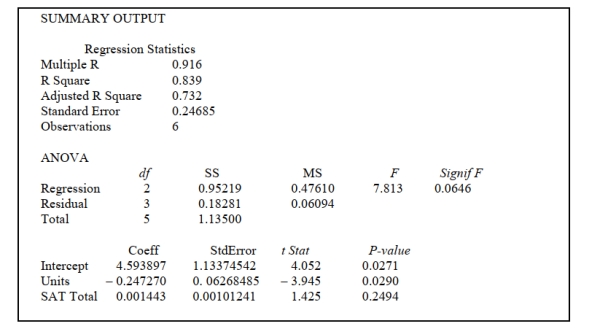-Referring to Scenario 14-7, the department head wants to use a t test to test for the significance of the coefficient of $X _ { 1 }$ . At a level of significance of 0.05, the department head would decide that $\beta _ { 1 } \neq 0$ .

SCENARIO 14-5 A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies. She proceeds to randomly select 26 large corporations and record information in millions of dollars. The Microsoft Excel output below shows results of this multiple regression. 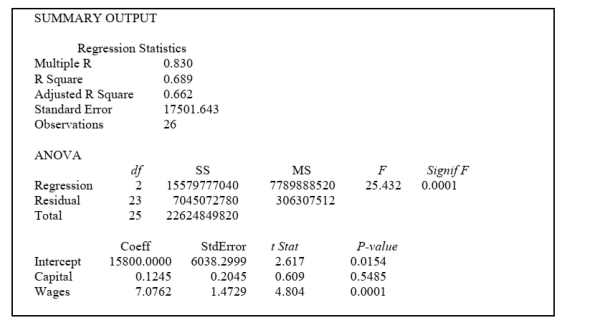-Referring to Scenario 14-5, which of the independent variables in the model are significant at the 5% level?

In a multiple regression model, which of the following is correct regarding the value of the adjusted r2 ?

SCENARIO 14-20-A You are the CEO of a dairy company. You are planning to expand milk production by purchasing additional cows, lands and hiring more workers. From the existing 50 farms owned by the company, you have collected data on total milk production (in liters), the number of milking cows, land size (in acres) and the number of laborers. The data are shown below and also available in the Excel file Scenario14-20-DataA.XLSX. S 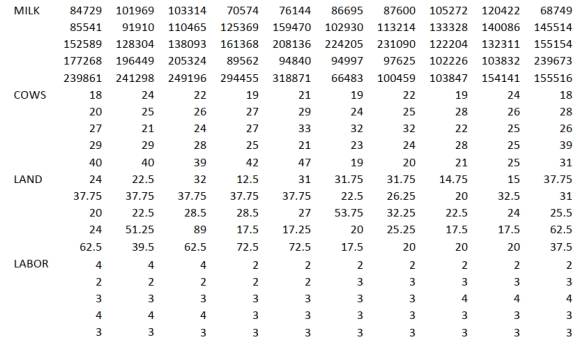You believe that the number of milking cows $\left( X _ { 1 } \right)$ , land size $\left( X _ { 2 } \right)$ and the number of laborers $\left( X _ { 3 } \right)$ are the best predictors for total milk production on any given farm. -Referring to Scenario 14-20-A, construct the residual plot for the number of laborers.

SCENARIO 14-13 An econometrician is interested in evaluating the relationship of demand for building materials to mortgage rates in Los Angeles and San Francisco. He believes that the appropriate model is $Y = 10 + 5 X _ { 1 } + 8 X _ { 2 }$ where where = mortgage rate in \% =1 if SF, 0 if LA Y= demand in \ 100 per capita -Referring to Scenario 14-13, the fitted model for predicting demand in San Francisco is ________. a) $10 + 5 X _ { 1 }$ b) $10 + 13 X _ { 1 }$ c) $15 + 8 X _ { 2 }$ d) $18 + 5 X _ { 1 }$

SCENARIO 14-20-A You are the CEO of a dairy company. You are planning to expand milk production by purchasing additional cows, lands and hiring more workers. From the existing 50 farms owned by the company, you have collected data on total milk production (in liters), the number of milking cows, land size (in acres) and the number of laborers. The data are shown below and also available in the Excel file Scenario14-20-DataA.XLSX. S You believe that the number of milking cows $\left( X _ { 1 } \right)$ , land size $\left( X _ { 2 } \right)$ and the number of laborers $\left( X _ { 3 } \right)$ are the best predictors for total milk production on any given farm. -Referring to Scenario 14-20-A, the estimated mean total milk production of a farm with 30 milking cows, 20 acres of land and 3 laborers is _____ liters.

A regression had the following results: SST = 82.55, SSE = 29.85. It can be said that 73.4% of the variation in the dependent variable is explained by the independent variables in the regression.

SCENARIO 14-5 A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies. She proceeds to randomly select 26 large corporations and record information in millions of dollars. The Microsoft Excel output below shows results of this multiple regression. -Referring to Scenario 14-5, what is the p-value for testing whether Wages have a positive impact on corporate sales?

SCENARIO 14-20-B You are the CEO of a dairy company. You are planning to expand milk production by purchasing additional cows, lands and hiring more workers. From the existing 50 farms owned by the company, you have collected data on total milk production (in liters), the number of milking cows, land size (in acres) and the number of laborers. The data are shown below and also available in the Excel file Scenario14-20-DataB.XLSX. MILK 84686 101876 103248 70508 76072 86615 87508 105195 120351 68658 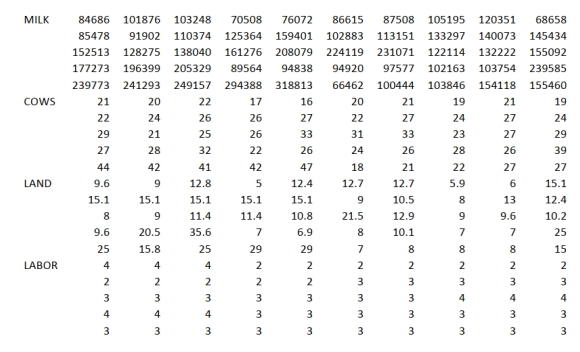You believe that the number of milking cows $\left( X _ { 1 } \right)$ , land size $\left( X _ { 2 } \right)$ and the number of laborers $\left( X _ { 3 } \right)$ are the best predictors for total milk production on any given farm. -Referring to Scenario 14-20-B, the null hypothesis should be rejected at a 1% level of significance when testing whether there is a significant relationship between total milk production and the entire set of explanatory variables.

SCENARIO 14-1 A manager of a product sales group believes the number of sales made by an employee $( Y )$ depends on how many years that employee has been with the company $\left( X _ { 1 } \right)$ and how he/she scored on a business aptitude test $\left( X _ { 2 } \right)$ . A random sample of 8 employees provides the following: 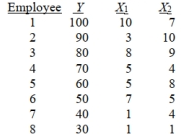-Referring to Scenario 14-1, for these data, what is the estimated coefficient for the variable representing scores on the aptitude test, b2?

If a categorical independent variable contains 4 categories, then _________ dummy variable(s) will be needed to uniquely represent these categories.

SCENARIO 14-8 A financial analyst wanted to examine the relationship between salary (in $\$ 1,000$ ) and 2 variables: age $\left(X_{1}=\mathrm{Age}\right)$ and experience in the field $\left(X_{2}=\right.$ Exper). He took a sample of 20 employees and obtained the following Microsoft Excel output: Regression Statistics Multiple R 0.8535 R Square 0.7284 Adjusted R Square 0.6964 Standard Error 10.5630 Observations 20 $\text { ANOVA }$ Coefficients Standard Error t Stat P-value Lower 95\% O5\% Intercept 1.5740 9.2723 0.1698 0.8672 -17.9888 21.1368 Age 1.3045 0.1956 6.6678 0.0000 0.8917 1.7173 Exper -0.1478 0.1944 -0.7604 0.4574 -0.5580 0.2624 Also the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848. -Referring to Scenario 14-8, the coefficient of partial determination $r _ { Y 1 \cdot 2 } ^ { 2 }$ ⋅ is ____.

SCENARIO 14-20-B You are the CEO of a dairy company. You are planning to expand milk production by purchasing additional cows, lands and hiring more workers. From the existing 50 farms owned by the company, you have collected data on total milk production (in liters), the number of milking cows, land size (in acres) and the number of laborers. The data are shown below and also available in the Excel file Scenario14-20-DataB.XLSX. MILK 84686 101876 103248 70508 76072 86615 87508 105195 120351 68658 You believe that the number of milking cows $\left( X _ { 1 } \right)$ , land size $\left( X _ { 2 } \right)$ and the number of laborers $\left( X _ { 3 } \right)$ are the best predictors for total milk production on any given farm. -Referring to Scenario 14-20-B, what is the value of the test statistic when testing whether the number of laborers has any effect on the total milk production while holding constant the effect of the other independent variable?

SCENARIO 14-18 A logistic regression model was estimated in order to predict the probability that a randomly chosen university or college would be a private university using information on mean total Scholastic Aptitude Test score (SAT) at the university or college and whether the TOEFL criterion is at least 90 (Toefl90 = 1 if yes, 0 otherwise.) The dependent variable, Y, is school type (Type = 1 if private and 0 otherwise). The PHStat output is given below: Binary Logistic Regression Predictor Coefficients SE Coef Z p -Value Intercept -3.9594 1.6741 -2.3650 0.0180 SAT 0.0028 0.0011 2.5459 0.0109 Toefl90:1 0.1928 0.5827 0.3309 0.7407 Deviance 101.9826 -Referring to Scenario 14-18, what is the estimated odds ratio for a school with a mean SAT score of 1100 and a TOEFL criterion that is not at least 90?

SCENARIO 14-10 You worked as an intern at We Always Win Car Insurance Company last summer. You notice that individual car insurance premiums depend very much on the age of the individual and the number of traffic tickets received by the individual. You performed a regression analysis in EXCEL and obtained the following partial information: Regression Statistics Multiple R 0.8546 R Square 0.7303 Adjusted R Square 0.6853 Standard Error 226.7502 Observations 15 $\text { ANOVA }$ Coefficients Standard Error tStat P-value Lower 99\% Upper 99\% Intercept 821.2617 161.9391 5.0714 0.0003 326.6124 1315.9111 Age -1.4061 2.5988 -0.5411 0.5984 -9.3444 6.5321 Tickets 243.4401 43.2470 5.6291 0.0001 111.3406 375.5396 -Referring to Scenario 14-10, the proportion of the total variability in insurance premiums that can be explained by AGE and TICKETS is _________.

SCENARIO 14-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth- grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending) of 47 schools in the state. Following is the multiple regression output with $Y = \%$ Passing as the dependent variable, $X _ { 1 } =$ Salaries and $X _ { 2 } =$ Spending: Regression Statistics Multiple R 0.4276 R Square 0.1828 Adjusted R Square 0.1457 Standard Error 5.7351 Observations 47 ANOVA Coefficients Standard Error t Stat \rho -value Lower 95\% Upper 95\% Intercept -72.9916 45.9106 -1.5899 0.1190 -165.5184 19.5352 Salary 2.7939 0.8974 3.1133 0.0032 0.9853 4.6025 Spending 0.3742 0.9782 0.3825 0.7039 -1.5972 2.3455 -Referring to Scenario 14-15, the null hypothesis $H _ { 0 } : \beta _ { 1 } = \beta _ { 2 } = 0$ implies that percentage of students passing the proficiency test is not related to one of the explanatory variables.

SCENARIO 14-4 A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size). House size is measured in hundreds of square feet and income is measured in thousands of dollars. The builder randomly selected 50 families and ran the multiple regression. Partial Microsoft Excel output is provided below: 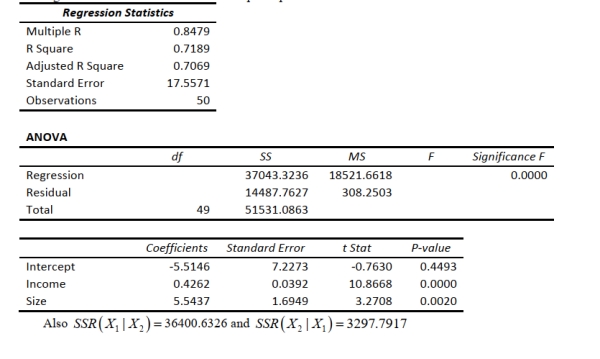-Referring to Scenario 14-4, which of the following values for the level of significance is the smallest for which the regression model as a whole is significant?

SCENARIO 14-16 What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 30 different vehicle models were collected: $Y$ (Accel Time): Acceleration time in sec. $X _ { I }$ (Engine Size): c.c. $X _ { 2 }$ (Sedan): 1 if the vehicle model is a sedan and 0 otherwise The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below. Regression Statistics Multiple R 0.6096 R Square 0.3716 Adjusted R Square 0.3251 Standard Error 1.4629 Observations 30 ANOVA Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 7.1052 0.6574 10.8086 0.0000 5.7564 8.4540 Engine Size -0.0005 0.0001 -3.6477 0.0011 -0.0008 -0.0002 Sedan 0.7264 0.5564 1.3056 0.2027 -0.4152 1.8681 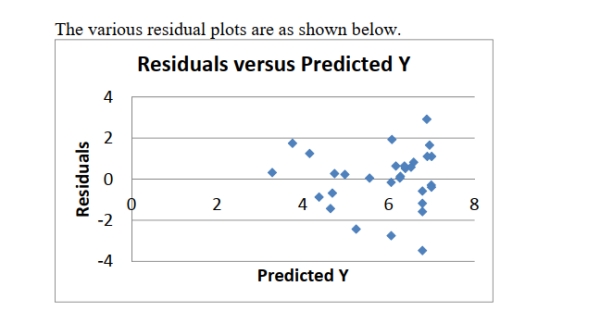-Referring to Scenario 14-16, the 0 to 60 miles per hour acceleration time of a sedan is predicted to be 0.7264 seconds higher than that of a non-sedan with the same engine size.

SCENARIO 14-2 A professor of industrial relations believes that an individual's wage rate at a factory $( Y )$ depends on his performance rating $\left( X _ { 1 } \right)$ and the number of economics courses the employee successfully completed in college $\left( X _ { 2 } \right)$ . The professor randomly selects 6 workers and collects the following information: 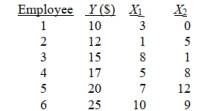-Referring to Scenario 14-2, suppose an employee had never taken an economics course and managed to score a 5 on his performance rating. What is his estimated expected wage rate?

SCENARIO 14-10 You worked as an intern at We Always Win Car Insurance Company last summer. You notice that individual car insurance premiums depend very much on the age of the individual and the number of traffic tickets received by the individual. You performed a regression analysis in EXCEL and obtained the following partial information: Regression Statistics Multiple R 0.8546 R Square 0.7303 Adjusted R Square 0.6853 Standard Error 226.7502 Observations 15 $\text { ANOVA }$ Coefficients Standard Error tStat P-value Lower 99\% Upper 99\% Intercept 821.2617 161.9391 5.0714 0.0003 326.6124 1315.9111 Age -1.4061 2.5988 -0.5411 0.5984 -9.3444 6.5321 Tickets 243.4401 43.2470 5.6291 0.0001 111.3406 375.5396 -Referring to Scenario 14-10, the multiple regression model is significant at a 10% level of significance.