Exam 14: Introduction to Multiple

SCENARIO 14-8 A financial analyst wanted to examine the relationship between salary (in $\$ 1,000$ ) and 2 variables: age $\left(X_{1}=\mathrm{Age}\right)$ and experience in the field $\left(X_{2}=\right.$ Exper). He took a sample of 20 employees and obtained the following Microsoft Excel output: Regression Statistics Multiple R 0.8535 R Square 0.7284 Adjusted R Square 0.6964 Standard Error 10.5630 Observations 20 $\text { ANOVA }$ Coefficients Standard Error t Stat P-value Lower 95\% O5\% Intercept 1.5740 9.2723 0.1698 0.8672 -17.9888 21.1368 Age 1.3045 0.1956 6.6678 0.0000 0.8917 1.7173 Exper -0.1478 0.1944 -0.7604 0.4574 -0.5580 0.2624 Also the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848. -Referring to Scenario 14-8, the estimated change in the mean salary (in $1,000) when an employee is a year older holding experience constant is ________.

SCENARIO 14-8 A financial analyst wanted to examine the relationship between salary (in $\$ 1,000$ ) and 2 variables: age $\left(X_{1}=\mathrm{Age}\right)$ and experience in the field $\left(X_{2}=\right.$ Exper). He took a sample of 20 employees and obtained the following Microsoft Excel output: Regression Statistics Multiple R 0.8535 R Square 0.7284 Adjusted R Square 0.6964 Standard Error 10.5630 Observations 20 $\text { ANOVA }$ Coefficients Standard Error t Stat P-value Lower 95\% O5\% Intercept 1.5740 9.2723 0.1698 0.8672 -17.9888 21.1368 Age 1.3045 0.1956 6.6678 0.0000 0.8917 1.7173 Exper -0.1478 0.1944 -0.7604 0.4574 -0.5580 0.2624 Also the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848. -Referring to Scenario 14-8, the critical value of an F test on the entire regression for a level of significance of 0.01 is ________.

SCENARIO 14-20-B You are the CEO of a dairy company. You are planning to expand milk production by purchasing additional cows, lands and hiring more workers. From the existing 50 farms owned by the company, you have collected data on total milk production (in liters), the number of milking cows, land size (in acres) and the number of laborers. The data are shown below and also available in the Excel file Scenario14-20-DataB.XLSX. MILK 84686 101876 103248 70508 76072 86615 87508 105195 120351 68658 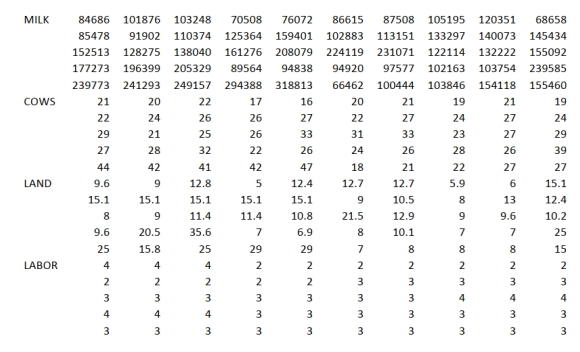You believe that the number of milking cows $\left( X _ { 1 } \right)$ , land size $\left( X _ { 2 } \right)$ and the number of laborers $\left( X _ { 3 } \right)$ are the best predictors for total milk production on any given farm. -Referring to Scenario 14-20-B, what are the lower and upper limits of the 95% confidence interval estimate for the change in mean total milk production as a result of adding one more acre of land after taking into consideration the effect of all the other independent variables?

SCENARIO 14-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth- grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending) of 47 schools in the state. Following is the multiple regression output with $Y = \%$ Passing as the dependent variable, $X _ { 1 } =$ Salaries and $X _ { 2 } =$ Spending: Regression Statistics Multiple R 0.4276 R Square 0.1828 Adjusted R Square 0.1457 Standard Error 5.7351 Observations 47 ANOVA Coefficients Standard Error t Stat \rho -value Lower 95\% Upper 95\% Intercept -72.9916 45.9106 -1.5899 0.1190 -165.5184 19.5352 Salary 2.7939 0.8974 3.1133 0.0032 0.9853 4.6025 Spending 0.3742 0.9782 0.3825 0.7039 -1.5972 2.3455 -Referring to Scenario 14-15, you can conclude definitively that mean teacher salary individually has no impact on the mean percentage of students passing the proficiency test, taking into account the effect of instructional spending per pupil, at a 1% level of significance based solely on but not actually computing the 99% confidence interval estimate for ?1.

14-30 Introduction to Multiple Regression 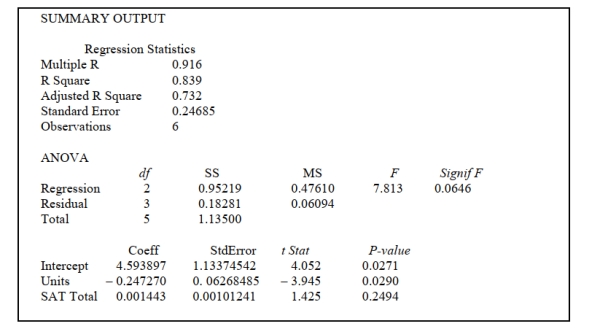-Referring to Scenario 14-7, the department head wants to test H0: $H _ { 0 } : \beta _ { 1 } = \beta _ { 2 } = 0$ . The appropriate alternative hypothesis is ________.

A regression had the following results: SST = 102.55, SSE = 82.04. It can be said that 90.0% of the variation in the dependent variable is explained by the independent variables in the regression.

SCENARIO 14-3 An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index). The Microsoft Excel output of this regression is partially reproduced below. 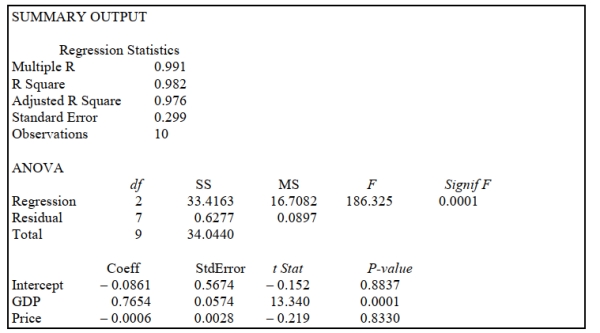-Referring to Scenario 14-3, what is the estimated mean consumption level for an economy with GDP equal to $2 billion and an aggregate price index of 90?

SCENARIO 14-14 An automotive engineer would like to be able to predict automobile mileages. She believes that the two most important characteristics that affect mileage are horsepower and the number of cylinders (4 or 6) of a car. She believes that the appropriate model is Y=40-0.05+20-0.1 where = horsepower =1 if 4 cylinders, 0 if 6 cylinders Y= mileage. -Referring to Scenario 14-14, the predicted mileage for a 200 horsepower, 4-cylinder car is ________.

SCENARIO 14-19 The marketing manager for a nationally franchised lawn service company would like to study the characteristics that differentiate home owners who do and do not have a lawn service. A random sample of 30 home owners located in a suburban area near a large city was selected; 11 did not have a lawn service (code 0) and 19 had a lawn service (code 1). Additional information available concerning these 30 home owners includes family income (Income, in thousands of dollars) and lawn size (Lawn Size, in thousands of square feet). The PHStat output is given below: Binary Logistic Regression Predictor Coefficients SE Coef Z p -Value Intercept -7.8562 3.8224 -2.0553 0.0398 Income 0.0304 0.0133 2.2897 0.0220 Lawn Size 1.2804 0.6971 1.8368 0.0662 Deviance 25.3089 -Referring to Scenario 14-19, what is the estimated odds ratio for a home owner with a family income of $50,000 and a lawn size of 5,000 square feet?

14-22 Introduction to Multiple Regression One of the most common questions of prospective house buyers pertains to the cost of heating in dollars $( Y )$ . To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit $\left( X _ { 1 } \right)$ and the amount of insulation in inches $\left( X _ { 2 } \right)$ . Given below is EXCEL output of the regression model. Regression Statistics Multiple R 0.5270 R Square 0.2778 Adjusted R Square 0.1928 Standard Error 40.9107 Observations 20 ANOVA Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 448.2925 90.7853 4.9379 0.0001 256.7522 639.8328 Temperature -2.7621 1.2371 -2.2327 0.0393 -5.3721 -0.1520 Insulation -15.9408 10.0638 -1.5840 0.1316 -37.1736 Also $\operatorname { SSR } \left( X _ { 1 } \mid X _ { 2 } \right) = 8343.3572$ and $\operatorname { SSR } \left( X _ { 2 } \mid X _ { 1 } \right) = 4199.2672$ -Referring to Scenario 14-6, the coefficient of partial determination $r _ { Y 1 \cdot 2 } ^ { 2 }$ ⋅ is ____.

From the coefficient of multiple determination, you cannot detect the strength of the relationship between Y and any individual independent variable.

14-30 Introduction to Multiple Regression -Referring to Scenario 14-7, the department head decided to construct a 95% confidence interval for $\beta _ { 1 }$ . The confidence interval is from ________ to ________.

SCENARIO 14-10 You worked as an intern at We Always Win Car Insurance Company last summer. You notice that individual car insurance premiums depend very much on the age of the individual and the number of traffic tickets received by the individual. You performed a regression analysis in EXCEL and obtained the following partial information: Regression Statistics Multiple R 0.8546 R Square 0.7303 Adjusted R Square 0.6853 Standard Error 226.7502 Observations 15 $\text { ANOVA }$ Coefficients Standard Error tStat P-value Lower 99\% Upper 99\% Intercept 821.2617 161.9391 5.0714 0.0003 326.6124 1315.9111 Age -1.4061 2.5988 -0.5411 0.5984 -9.3444 6.5321 Tickets 243.4401 43.2470 5.6291 0.0001 111.3406 375.5396 -Referring to Scenario 14-10, the proportion of the total variability in insurance premiums that can be explained by AGE and TICKETS after adjusting for the number of observations and the number independent variables is _________.

SCENARIO 14-3 An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index). The Microsoft Excel output of this regression is partially reproduced below. -Referring to Scenario 14-3, to test whether aggregate price index has a negative impact on consumption, the p-value is _______?

SCENARIO 14-8 A financial analyst wanted to examine the relationship between salary (in $\$ 1,000$ ) and 2 variables: age $\left(X_{1}=\mathrm{Age}\right)$ and experience in the field $\left(X_{2}=\right.$ Exper). He took a sample of 20 employees and obtained the following Microsoft Excel output: Regression Statistics Multiple R 0.8535 R Square 0.7284 Adjusted R Square 0.6964 Standard Error 10.5630 Observations 20 $\text { ANOVA }$ Coefficients Standard Error t Stat P-value Lower 95\% O5\% Intercept 1.5740 9.2723 0.1698 0.8672 -17.9888 21.1368 Age 1.3045 0.1956 6.6678 0.0000 0.8917 1.7173 Exper -0.1478 0.1944 -0.7604 0.4574 -0.5580 0.2624 Also the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848. -Referring to Scenario 14-8, the analyst wants to use a t test to test for the significance of the coefficient of $X _ { 2 }$ . The value of the test statistic is ________.

SCENARIO 14-19 The marketing manager for a nationally franchised lawn service company would like to study the characteristics that differentiate home owners who do and do not have a lawn service. A random sample of 30 home owners located in a suburban area near a large city was selected; 11 did not have a lawn service (code 0) and 19 had a lawn service (code 1). Additional information available concerning these 30 home owners includes family income (Income, in thousands of dollars) and lawn size (Lawn Size, in thousands of square feet). The PHStat output is given below: Binary Logistic Regression Predictor Coefficients SE Coef Z p -Value Intercept -7.8562 3.8224 -2.0553 0.0398 Income 0.0304 0.0133 2.2897 0.0220 Lawn Size 1.2804 0.6971 1.8368 0.0662 Deviance 25.3089 -Referring to Scenario 14-19, what is the estimated probability that a home owner with a family income of $50,000 and a lawn size of 2,000 square feet will purchase a lawn service?

SCENARIO 14-20-B You are the CEO of a dairy company. You are planning to expand milk production by purchasing additional cows, lands and hiring more workers. From the existing 50 farms owned by the company, you have collected data on total milk production (in liters), the number of milking cows, land size (in acres) and the number of laborers. The data are shown below and also available in the Excel file Scenario14-20-DataB.XLSX. MILK 84686 101876 103248 70508 76072 86615 87508 105195 120351 68658 You believe that the number of milking cows $\left( X _ { 1 } \right)$ , land size $\left( X _ { 2 } \right)$ and the number of laborers $\left( X _ { 3 } \right)$ are the best predictors for total milk production on any given farm. -Referring to Scenario 14-20-B, there is sufficient evidence that total milk production depends on each of the explanatory variables at a 1% level of significance when testing whether there is a significant relationship between total milk production and the entire set of explanatory variables.

14-30 Introduction to Multiple Regression -Referring to Scenario 14-7, the value of the coefficient of multiple determination, $r ^ { 2 } Y .12$ , is ________.

SCENARIO 14-4 A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size). House size is measured in hundreds of square feet and income is measured in thousands of dollars. The builder randomly selected 50 families and ran the multiple regression. Partial Microsoft Excel output is provided below: 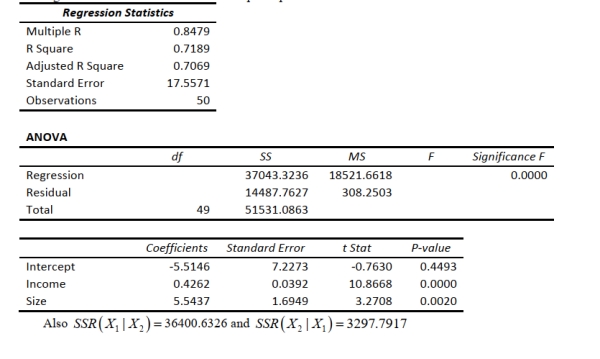-Referring to Scenario 14-4, the value of the partial F test statistic is ____ for $H _ { 0 }$ : Variable $X _ { 1 }$ does not significantly improve the model after variable $X _ { 2 }$ has been included $H _ { 1 }$ : Variable $X _ { 1 }$ significantly improves the model after variable $X _ { 2 }$ has been included

14-22 Introduction to Multiple Regression One of the most common questions of prospective house buyers pertains to the cost of heating in dollars $( Y )$ . To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit $\left( X _ { 1 } \right)$ and the amount of insulation in inches $\left( X _ { 2 } \right)$ . Given below is EXCEL output of the regression model. Regression Statistics Multiple R 0.5270 R Square 0.2778 Adjusted R Square 0.1928 Standard Error 40.9107 Observations 20 ANOVA Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 448.2925 90.7853 4.9379 0.0001 256.7522 639.8328 Temperature -2.7621 1.2371 -2.2327 0.0393 -5.3721 -0.1520 Insulation -15.9408 10.0638 -1.5840 0.1316 -37.1736 Also $\operatorname { SSR } \left( X _ { 1 } \mid X _ { 2 } \right) = 8343.3572$ and $\operatorname { SSR } \left( X _ { 2 } \mid X _ { 1 } \right) = 4199.2672$ -Referring to Scenario 14-6, the value of the partial F test statistic is ____ for $H _ { 0 }$ : Variable $X _ { 2 }$ does not significantly improve the model after variable $X _ { l }$ has been included $H _ { 1 }$ : Variable $X _ { 2 }$ significantly improves the model after variable $X _ { 1 }$ has been included