Exam 14: Introduction to Multiple
Exam 1: Defining and Collecting Data202 Questions
Exam 2: Organizing and Visualizing256 Questions
Exam 3: Numerical Descriptive Measures217 Questions
Exam 4: Basic Probability167 Questions
Exam 5: Discrete Probability Distributions165 Questions
Exam 6: The Normal Distribution and Other Continuous Distributions170 Questions
Exam 7: Sampling Distributions165 Questions
Exam 8: Confidence Interval Estimation219 Questions
Exam 9: Fundamentals of Hypothesis Testing: One-Sample Tests194 Questions
Exam 10: Two-Sample Tests240 Questions
Exam 11: Analysis of Variance170 Questions
Exam 12: Chi-Square and Nonparametric188 Questions
Exam 13: Simple Linear Regression243 Questions
Exam 14: Introduction to Multiple394 Questions
Exam 15: Multiple Regression146 Questions
Exam 16: Time-Series Forecasting235 Questions
Exam 17: Getting Ready to Analyze Data386 Questions
Exam 18: Statistical Applications in Quality Management159 Questions
Exam 19: Decision Making126 Questions
Exam 20: Probability and Combinatorics421 Questions
Select questions type
SCENARIO 14-20-A
You are the CEO of a dairy company. You are planning to expand milk production by purchasing
additional cows, lands and hiring more workers. From the existing 50 farms owned by the company,
you have collected data on total milk production (in liters), the number of milking cows, land size (in
acres) and the number of laborers. The data are shown below and also available in the Excel file
Scenario14-20-DataA.XLSX.
S 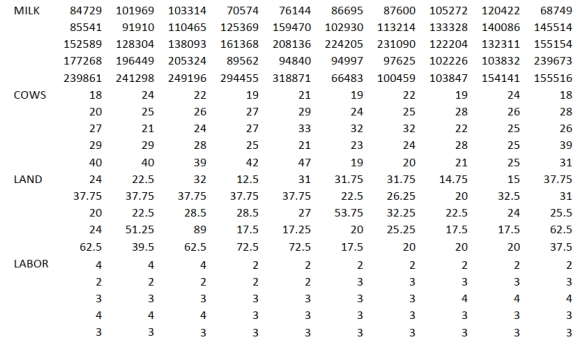 You believe that the number of milking cows , land size and the number of laborers are the best predictors for total milk production on any given farm.
-Referring to Scenario 14-20-A, what is the value of the coefficient of partial determination ?
You believe that the number of milking cows , land size and the number of laborers are the best predictors for total milk production on any given farm.
-Referring to Scenario 14-20-A, what is the value of the coefficient of partial determination ?
(Short Answer)
4.8/5  (37)
(37)
SCENARIO 14-17
Given below are results from the regression analysis where the dependent variable is the number of
weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age
of the worker (Age) and a dummy variable for management position (Manager: 1 = yes, 0 = no).
The results of the regression analysis are given below: \ Regression Statistics Multiple R 0.6391 R Square 0.4085 Adjusted R Square 0.3765 Standard Error 18.8929 Observations 40
 Coefficients Standard Error t Stat P-value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541
-Referring to Scenario 14-17, which of the following is the correct null hypothesis to test whether age has any effect on the number of weeks a worker is unemployed due to a layoff while
Holding constant the effect of the other independent variable? a)
b)
c)
d)
Coefficients Standard Error t Stat P-value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541
-Referring to Scenario 14-17, which of the following is the correct null hypothesis to test whether age has any effect on the number of weeks a worker is unemployed due to a layoff while
Holding constant the effect of the other independent variable? a)
b)
c)
d)
(Short Answer)
4.8/5  (33)
(33)
SCENARIO 14-20-A
You are the CEO of a dairy company. You are planning to expand milk production by purchasing
additional cows, lands and hiring more workers. From the existing 50 farms owned by the company,
you have collected data on total milk production (in liters), the number of milking cows, land size (in
acres) and the number of laborers. The data are shown below and also available in the Excel file
Scenario14-20-DataA.XLSX.
S  You believe that the number of milking cows , land size and the number of laborers are the best predictors for total milk production on any given farm.
-Referring to Scenario 14-20-A, there is sufficient evidence that all of the
explanatory variables affect total milk production at a 1% level of significance when testing
whether there is a significant relationship between total milk production and the entire set of
explanatory variables.
You believe that the number of milking cows , land size and the number of laborers are the best predictors for total milk production on any given farm.
-Referring to Scenario 14-20-A, there is sufficient evidence that all of the
explanatory variables affect total milk production at a 1% level of significance when testing
whether there is a significant relationship between total milk production and the entire set of
explanatory variables.
(True/False)
4.9/5  (26)
(26)
SCENARIO 14-10
You worked as an intern at We Always Win Car Insurance Company last summer. You notice that
individual car insurance premiums depend very much on the age of the individual and the number of
traffic tickets received by the individual. You performed a regression analysis in EXCEL and
obtained the following partial information: Regression Statistics Multiple R 0.8546 R Square 0.7303 Adjusted R Square 0.6853 Standard Error 226.7502 Observations 15
 Coefficients Standard Error tStat P-value Lower 99\% Upper 99\% Intercept 821.2617 161.9391 5.0714 0.0003 326.6124 1315.9111 Age -1.4061 2.5988 -0.5411 0.5984 -9.3444 6.5321 Tickets 243.4401 43.2470 5.6291 0.0001 111.3406 375.5396
-Referring to Scenario 14-10, to test the significance of the multiple regression model, what is the form of the null hypothesis? a)
b)
c)
d)
Coefficients Standard Error tStat P-value Lower 99\% Upper 99\% Intercept 821.2617 161.9391 5.0714 0.0003 326.6124 1315.9111 Age -1.4061 2.5988 -0.5411 0.5984 -9.3444 6.5321 Tickets 243.4401 43.2470 5.6291 0.0001 111.3406 375.5396
-Referring to Scenario 14-10, to test the significance of the multiple regression model, what is the form of the null hypothesis? a)
b)
c)
d)
(Short Answer)
4.9/5  (43)
(43)
When a dummy variable is included in a multiple regression model, the
interpretation of the estimated slope coefficient does not make any sense anymore.
(True/False)
4.8/5  (26)
(26)
SCENARIO 14-20-A
You are the CEO of a dairy company. You are planning to expand milk production by purchasing
additional cows, lands and hiring more workers. From the existing 50 farms owned by the company,
you have collected data on total milk production (in liters), the number of milking cows, land size (in
acres) and the number of laborers. The data are shown below and also available in the Excel file
Scenario14-20-DataA.XLSX.
S  You believe that the number of milking cows , land size and the number of laborers are the best predictors for total milk production on any given farm.
-Referring to Scenario 14-20-A, the null hypothesis should be rejected at a 1%
level of significance when testing whether there is a significant relationship between total milk
production and the entire set of explanatory variables.
You believe that the number of milking cows , land size and the number of laborers are the best predictors for total milk production on any given farm.
-Referring to Scenario 14-20-A, the null hypothesis should be rejected at a 1%
level of significance when testing whether there is a significant relationship between total milk
production and the entire set of explanatory variables.
(True/False)
4.8/5  (33)
(33)
SCENARIO 14-16
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a
car? Data on the following variables for 30 different vehicle models were collected: (Accel Time): Acceleration time in sec.
(Engine Size): c.c.
(Sedan): 1 if the vehicle model is a sedan and 0 otherwise
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
Regression Statistics Multiple R 0.6096 R Square 0.3716 Adjusted R Square 0.3251 Standard Error 1.4629 Observations 30
ANOVA
 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 7.1052 0.6574 10.8086 0.0000 5.7564 8.4540 Engine Size -0.0005 0.0001 -3.6477 0.0011 -0.0008 -0.0002 Sedan 0.7264 0.5564 1.3056 0.2027 -0.4152 1.8681
Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 7.1052 0.6574 10.8086 0.0000 5.7564 8.4540 Engine Size -0.0005 0.0001 -3.6477 0.0011 -0.0008 -0.0002 Sedan 0.7264 0.5564 1.3056 0.2027 -0.4152 1.8681
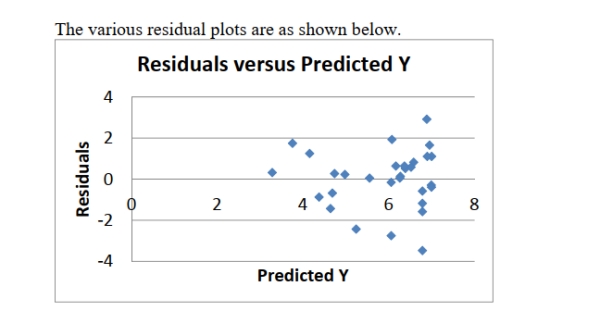 -Referring to Scenario 14-16, which of the following assumptions is most likely violated based on the residual plot for Engine Size?
-Referring to Scenario 14-16, which of the following assumptions is most likely violated based on the residual plot for Engine Size?
(Multiple Choice)
4.9/5  (30)
(30)
SCENARIO 14-20-A
You are the CEO of a dairy company. You are planning to expand milk production by purchasing
additional cows, lands and hiring more workers. From the existing 50 farms owned by the company,
you have collected data on total milk production (in liters), the number of milking cows, land size (in
acres) and the number of laborers. The data are shown below and also available in the Excel file
Scenario14-20-DataA.XLSX.
S  You believe that the number of milking cows , land size and the number of laborers are the best predictors for total milk production on any given farm.
-Referring to Scenario 14-20-A, which of the following is a correct interpretation for the r- square?
You believe that the number of milking cows , land size and the number of laborers are the best predictors for total milk production on any given farm.
-Referring to Scenario 14-20-A, which of the following is a correct interpretation for the r- square?
(Multiple Choice)
5.0/5  (32)
(32)
SCENARIO 14-8 A financial analyst wanted to examine the relationship between salary (in ) and 2 variables: age and experience in the field Exper). He took a sample of 20 employees and obtained the following Microsoft Excel output:
Regression Statistics Multiple R 0.8535 R Square 0.7284 Adjusted R Square 0.6964 Standard Error 10.5630 Observations 20
 Coefficients Standard Error t Stat P-value Lower 95\% O5\% Intercept 1.5740 9.2723 0.1698 0.8672 -17.9888 21.1368 Age 1.3045 0.1956 6.6678 0.0000 0.8917 1.7173 Exper -0.1478 0.1944 -0.7604 0.4574 -0.5580 0.2624
Also the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the
sum of squares due to the regression for the model that includes only Exper is 125.9848.
-Referring to Scenario 14-8, the analyst wants to use a t test to test for the significance of the
coefficient of . The p-value of the test is ________.
Coefficients Standard Error t Stat P-value Lower 95\% O5\% Intercept 1.5740 9.2723 0.1698 0.8672 -17.9888 21.1368 Age 1.3045 0.1956 6.6678 0.0000 0.8917 1.7173 Exper -0.1478 0.1944 -0.7604 0.4574 -0.5580 0.2624
Also the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the
sum of squares due to the regression for the model that includes only Exper is 125.9848.
-Referring to Scenario 14-8, the analyst wants to use a t test to test for the significance of the
coefficient of . The p-value of the test is ________.
(Short Answer)
4.9/5  (33)
(33)
SCENARIO 14-20-B
You are the CEO of a dairy company. You are planning to expand milk production by purchasing
additional cows, lands and hiring more workers. From the existing 50 farms owned by the company,
you have collected data on total milk production (in liters), the number of milking cows, land size (in
acres) and the number of laborers. The data are shown below and also available in the Excel file
Scenario14-20-DataB.XLSX.
MILK 84686 101876 103248 70508 76072 86615 87508 105195 120351 68658 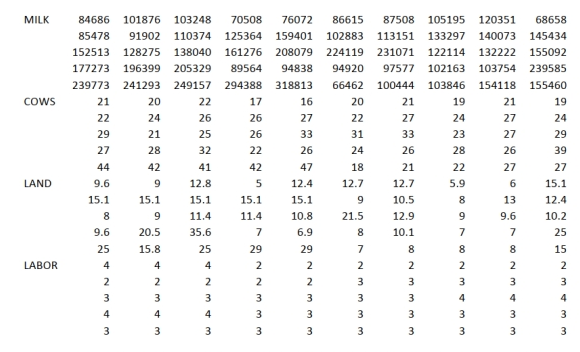 You believe that the number of milking cows , land size and the number of laborers are the best predictors for total milk production on any given farm.
-Referring to Scenario 14-20-B, the predicted total milk production of a farm with 40 milking
cows, 30 acres of land and 3 laborers is _____ liters.
You believe that the number of milking cows , land size and the number of laborers are the best predictors for total milk production on any given farm.
-Referring to Scenario 14-20-B, the predicted total milk production of a farm with 40 milking
cows, 30 acres of land and 3 laborers is _____ liters.
(Short Answer)
4.8/5  (34)
(34)
SCENARIO 14-20-A
You are the CEO of a dairy company. You are planning to expand milk production by purchasing
additional cows, lands and hiring more workers. From the existing 50 farms owned by the company,
you have collected data on total milk production (in liters), the number of milking cows, land size (in
acres) and the number of laborers. The data are shown below and also available in the Excel file
Scenario14-20-DataA.XLSX.
S  You believe that the number of milking cows , land size and the number of laborers are the best predictors for total milk production on any given farm.
-Referring to Scenario 14-20-A, what is the value of the coefficient of partial determination ?
You believe that the number of milking cows , land size and the number of laborers are the best predictors for total milk production on any given farm.
-Referring to Scenario 14-20-A, what is the value of the coefficient of partial determination ?
(Short Answer)
4.9/5  (30)
(30)
SCENARIO 14-4
A real estate builder wishes to determine how house size (House) is influenced by family income
(Income) and family size (Size). House size is measured in hundreds of square feet and income is
measured in thousands of dollars. The builder randomly selected 50 families and ran the multiple
regression. Partial Microsoft Excel output is provided below: 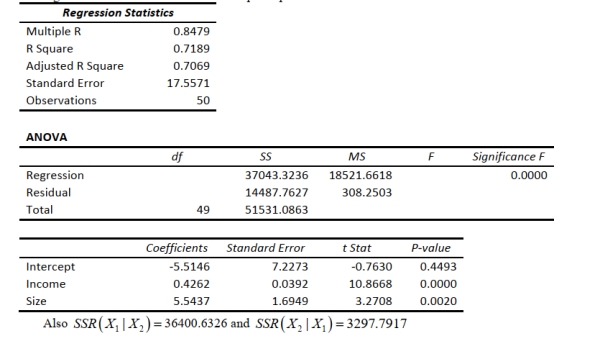 -Referring to Scenario 14-4, at the 0.01 level of significance, what conclusion should the builder draw regarding the inclusion of Size in the regression model?
-Referring to Scenario 14-4, at the 0.01 level of significance, what conclusion should the builder draw regarding the inclusion of Size in the regression model?
(Multiple Choice)
4.9/5  (29)
(29)
When an explanatory variable is dropped from a multiple regression model, the
coefficient of multiple determination can increase.
(True/False)
4.7/5  (39)
(39)
SCENARIO 14-20-A
You are the CEO of a dairy company. You are planning to expand milk production by purchasing
additional cows, lands and hiring more workers. From the existing 50 farms owned by the company,
you have collected data on total milk production (in liters), the number of milking cows, land size (in
acres) and the number of laborers. The data are shown below and also available in the Excel file
Scenario14-20-DataA.XLSX.
S  You believe that the number of milking cows , land size and the number of laborers are the best predictors for total milk production on any given farm.
-Referring to Scenario 14-20-A, there is sufficient evidence that the number of
milking cows has an effect on the total milk production while holding constant the effect of the
other independent variables at a 10% level of significance.
You believe that the number of milking cows , land size and the number of laborers are the best predictors for total milk production on any given farm.
-Referring to Scenario 14-20-A, there is sufficient evidence that the number of
milking cows has an effect on the total milk production while holding constant the effect of the
other independent variables at a 10% level of significance.
(True/False)
4.7/5  (40)
(40)
SCENARIO 14-17
Given below are results from the regression analysis where the dependent variable is the number of
weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age
of the worker (Age) and a dummy variable for management position (Manager: 1 = yes, 0 = no).
The results of the regression analysis are given below: \ Regression Statistics Multiple R 0.6391 R Square 0.4085 Adjusted R Square 0.3765 Standard Error 18.8929 Observations 40
 Coefficients Standard Error t Stat P-value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541
-Referring to Scenario 14-17, we can conclude definitively that, holding constant
the effect of the other independent variables, there is not a difference in the mean number of
weeks a worker is unemployed due to a layoff between a worker who is in a management position
and one who is not at a 1% level of significance if all we have is the information of the 95%
confidence interval estimate for the difference in the mean number of weeks a worker is
unemployed due to a layoff between a worker who is in a management position and one who is
not.
Coefficients Standard Error t Stat P-value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541
-Referring to Scenario 14-17, we can conclude definitively that, holding constant
the effect of the other independent variables, there is not a difference in the mean number of
weeks a worker is unemployed due to a layoff between a worker who is in a management position
and one who is not at a 1% level of significance if all we have is the information of the 95%
confidence interval estimate for the difference in the mean number of weeks a worker is
unemployed due to a layoff between a worker who is in a management position and one who is
not.
(True/False)
4.8/5  (34)
(34)
SCENARIO 14-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage
spending by companies. She proceeds to randomly select 26 large corporations and record
information in millions of dollars. The Microsoft Excel output below shows results of this multiple
regression. 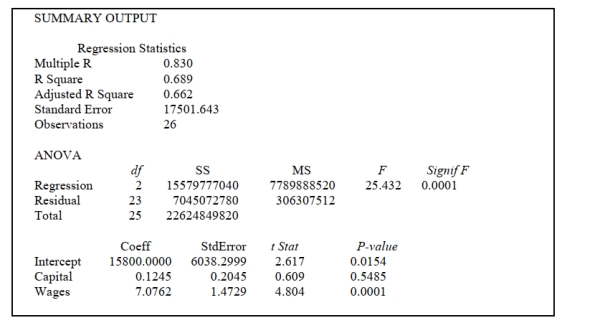 -Referring to Scenario 14-5, at the 0.01 level of significance, what conclusion should the microeconomist reach regarding the inclusion of Capital in the regression model?
-Referring to Scenario 14-5, at the 0.01 level of significance, what conclusion should the microeconomist reach regarding the inclusion of Capital in the regression model?
(Multiple Choice)
4.9/5  (40)
(40)
SCENARIO 14-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-
grade proficiency test. She obtained the data on percentage of students passing the proficiency test
(% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per
pupil in thousands of dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Passing as the dependent variable,
Salaries and Spending:
Regression Statistics Multiple R 0.4276 R Square 0.1828 Adjusted R Square 0.1457 Standard Error 5.7351 Observations 47
ANOVA
 Coefficients Standard Error t Stat \rho -value Lower 95\% Upper 95\% Intercept -72.9916 45.9106 -1.5899 0.1190 -165.5184 19.5352 Salary 2.7939 0.8974 3.1133 0.0032 0.9853 4.6025 Spending 0.3742 0.9782 0.3825 0.7039 -1.5972 2.3455
-Referring to Scenario 14-15, what is the standard error of estimate?
Coefficients Standard Error t Stat \rho -value Lower 95\% Upper 95\% Intercept -72.9916 45.9106 -1.5899 0.1190 -165.5184 19.5352 Salary 2.7939 0.8974 3.1133 0.0032 0.9853 4.6025 Spending 0.3742 0.9782 0.3825 0.7039 -1.5972 2.3455
-Referring to Scenario 14-15, what is the standard error of estimate?
(Short Answer)
4.8/5  (43)
(43)
SCENARIO 14-17
Given below are results from the regression analysis where the dependent variable is the number of
weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age
of the worker (Age) and a dummy variable for management position (Manager: 1 = yes, 0 = no).
The results of the regression analysis are given below: \ Regression Statistics Multiple R 0.6391 R Square 0.4085 Adjusted R Square 0.3765 Standard Error 18.8929 Observations 40
 Coefficients Standard Error t Stat P-value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541
-Referring to Scenario 14-17, what is the value of the test statistic when testing whether age has
any effect on the number of weeks a worker is unemployed due to a layoff while holding constant
the effect of the other independent variable?
Coefficients Standard Error t Stat P-value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541
-Referring to Scenario 14-17, what is the value of the test statistic when testing whether age has
any effect on the number of weeks a worker is unemployed due to a layoff while holding constant
the effect of the other independent variable?
(Short Answer)
4.7/5  (32)
(32)
SCENARIO 14-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by
gross domestic product ($ billions) and aggregate price (consumer price index). The Microsoft Excel
output of this regression is partially reproduced below. 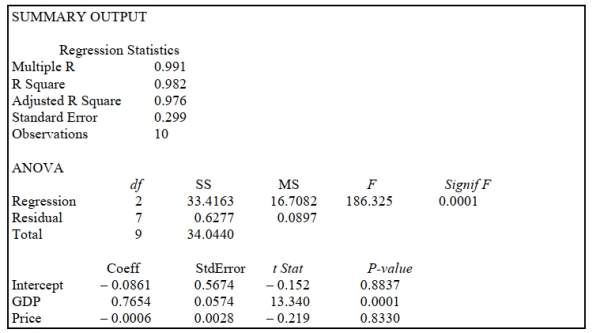 -Referring to Scenario 14-3, to test for the significance of the coefficient on gross domestic product, the p-value is
-Referring to Scenario 14-3, to test for the significance of the coefficient on gross domestic product, the p-value is
(Multiple Choice)
4.7/5  (29)
(29)
SCENARIO 14-10
You worked as an intern at We Always Win Car Insurance Company last summer. You notice that
individual car insurance premiums depend very much on the age of the individual and the number of
traffic tickets received by the individual. You performed a regression analysis in EXCEL and
obtained the following partial information: Regression Statistics Multiple R 0.8546 R Square 0.7303 Adjusted R Square 0.6853 Standard Error 226.7502 Observations 15
 Coefficients Standard Error tStat P-value Lower 99\% Upper 99\% Intercept 821.2617 161.9391 5.0714 0.0003 326.6124 1315.9111 Age -1.4061 2.5988 -0.5411 0.5984 -9.3444 6.5321 Tickets 243.4401 43.2470 5.6291 0.0001 111.3406 375.5396
-Referring to Scenario 14-10, the total degrees of freedom that are missing in the ANOVA table
should be ______.
Coefficients Standard Error tStat P-value Lower 99\% Upper 99\% Intercept 821.2617 161.9391 5.0714 0.0003 326.6124 1315.9111 Age -1.4061 2.5988 -0.5411 0.5984 -9.3444 6.5321 Tickets 243.4401 43.2470 5.6291 0.0001 111.3406 375.5396
-Referring to Scenario 14-10, the total degrees of freedom that are missing in the ANOVA table
should be ______.
(Short Answer)
4.8/5  (30)
(30)
Showing 201 - 220 of 394
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)