Exam 20: Probability and Combinatorics
Exam 1: Defining and Collecting Data202 Questions
Exam 2: Organizing and Visualizing256 Questions
Exam 3: Numerical Descriptive Measures217 Questions
Exam 4: Basic Probability167 Questions
Exam 5: Discrete Probability Distributions165 Questions
Exam 6: The Normal Distribution and Other Continuous Distributions170 Questions
Exam 7: Sampling Distributions165 Questions
Exam 8: Confidence Interval Estimation219 Questions
Exam 9: Fundamentals of Hypothesis Testing: One-Sample Tests194 Questions
Exam 10: Two-Sample Tests240 Questions
Exam 11: Analysis of Variance170 Questions
Exam 12: Chi-Square and Nonparametric188 Questions
Exam 13: Simple Linear Regression243 Questions
Exam 14: Introduction to Multiple394 Questions
Exam 15: Multiple Regression146 Questions
Exam 16: Time-Series Forecasting235 Questions
Exam 17: Getting Ready to Analyze Data386 Questions
Exam 18: Statistical Applications in Quality Management159 Questions
Exam 19: Decision Making126 Questions
Exam 20: Probability and Combinatorics421 Questions
Select questions type
A company that receives the majority of its orders by telephone conducted a study to determine how long customers were willing to wait on hold before ordering a product. The length of waiting
Time was found to be a variable best approximated by an exponential distribution with a mean
Length of waiting time equal to 3 minutes (i.e. the mean number of calls answered in a minute is
1/3). What proportion of customers having to hold more than 1.5 minutes will hang up before
Placing an order?
(Multiple Choice)
4.8/5  (29)
(29)
SCENARIO 4-15
At a Texas college, 60% of the students are from the southern part of the state, 30% are from the
northern part of the state, and the remaining 10% are from out-of-state. All students must take and
pass an Entry Level Math (ELM) test. 60% of the southerners have passed the ELM, 70% of the
northerners have passed the ELM, and 90% of the out-of-staters have passed the ELM.
-Referring to Scenario 4-15, if a randomly selected student has passed the ELM, the probability
the student is from out-of-state is ________.
(Short Answer)
4.8/5  (33)
(33)
To determine the probability of getting more than 3 events of interest in a binomial
distribution, you will find the area under the normal curve for X = 3.5 and above.
(True/False)
4.8/5  (26)
(26)
SCENARIO 8-14
The president of a university is concerned that the percentage of students who have cheated on an
exam is higher than the 1% acceptable level. A confidential random sample of 1,000 students from a
population of 7,000 revealed that 6 of them said that they had cheated on an exam during the last
semester.
-Referring to Scenario 8-14, the president can be 90% confident that no more than 1%
of the students at the university had cheated on an exam during the last semester.
(True/False)
4.7/5  (32)
(32)
SCENARIO 6-8
A company has 125 personal computers. The probability that any one of them will require repair on a
given day is 0.15.
-Referring to Scenario 6-8 and assuming that the number of computers that requires repair on a
given day follows a binomial distribution, compute the probability that there will be no more than
8 computers that require repair on a given day using a normal approximation.
(Short Answer)
4.7/5  (37)
(37)
A company that receives the majority of its orders by telephone conducted a study to determine how long customers were willing to wait on hold before ordering a product. The length of waiting
Time was found to be a variable best approximated by an exponential distribution with a mean
Length of waiting time equal to 3 minutes (i.e. the mean number of calls answered in a minute is
1/3). What proportion of customers having to hold more than 4.5 minutes will hang up before
Placing an order?
(Multiple Choice)
4.8/5  (34)
(34)
To determine the probability of getting between 3 and 4 events of interest in a
binomial distribution, you will find the area under the normal curve between X = 3.5 and 4.5.
(True/False)
4.7/5  (42)
(42)
The interval between patients arriving at an outpatient clinic follows an exponential distribution
at a rate of 15 patients per hour. What is the probability that a randomly chosen arrival to be
less than 15 minutes?
(Short Answer)
4.8/5  (41)
(41)
SCENARIO 9-11
An appliance manufacturer claims to have developed a compact microwave oven that consumes a
population mean of no more than 250 W. From previous studies, it is believed that power
consumption for microwave ovens is normally distributed with a population standard deviation of 15
W. If there is evidence that the population mean consumption is greater than 250 W, the manufacturer
will be unable to make the claim.
-Referring to Scenario 9-11, if you select a sample of 20 compact microwave ovens and are
willing to have a level of significance of 0.05, the probability of making a Type II error is _____
if the mean power consumption of all such microwave ovens is in fact 257.3 W.
(Short Answer)
4.8/5  (34)
(34)
SCENARIO 11-12
A student team in a business statistics course designed an experiment to investigate whether the brand
of bubblegum used affected the size of bubbles they could blow. To reduce the person-to-person
variability, the students decided to use a randomized block design using themselves as blocks.
Four brands of bubblegum were tested. A student chewed two pieces of a brand of gum and then blew
a bubble, attempting to make it as big as possible. Another student measured the diameter of the
bubble at its biggest point. The following table gives the diameters of the bubbles (in inches) for the
16 observations. 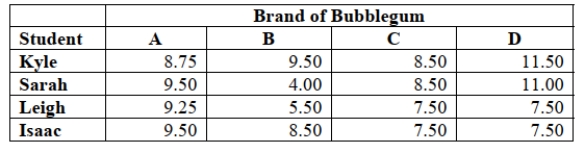 -Referring to Scenario 11-12, the randomized block F test is valid only if the
population of diameters is normally distributed for the 4 brands.
-Referring to Scenario 11-12, the randomized block F test is valid only if the
population of diameters is normally distributed for the 4 brands.
(True/False)
4.8/5  (34)
(34)
SCENARIO 5-11
There are two houses with almost identical characteristics available for investment in two different
neighborhoods with drastically different demographic composition. The anticipated gain in value
when the houses are sold in 10 years has the following probability distribution: 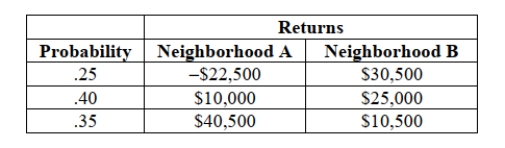 -Referring to Scenario 5-11, if you can invest 90% of your money on the house in neighborhood A
and the remaining on the house in neighborhood B, what is the portfolio expected return of your
investment?
-Referring to Scenario 5-11, if you can invest 90% of your money on the house in neighborhood A
and the remaining on the house in neighborhood B, what is the portfolio expected return of your
investment?
(Short Answer)
4.8/5  (41)
(41)
SCENARIO 5-11
There are two houses with almost identical characteristics available for investment in two different
neighborhoods with drastically different demographic composition. The anticipated gain in value
when the houses are sold in 10 years has the following probability distribution:  -Referring to Scenario 5-11, if you can invest half of your money on the house in neighborhood A
and the remaining on the house in neighborhood B, what is the portfolio risk of your investment?
-Referring to Scenario 5-11, if you can invest half of your money on the house in neighborhood A
and the remaining on the house in neighborhood B, what is the portfolio risk of your investment?
(Short Answer)
4.8/5  (36)
(36)
SCENARIO 5-13
From an inventory of 48 new cars being shipped to local dealerships, corporate reports indicate that
12 have defective radios installed.
-Referring to Scenario 5-13, what is the probability out of the 8 new cars it just received that,
when each is tested, none of the cars have defective radios?
(Short Answer)
4.7/5  (39)
(39)
SCENARIO 6-8
A company has 125 personal computers. The probability that any one of them will require repair on a
given day is 0.15.
-Referring to Scenario 6-8 and assuming that the number of computers that requires repair on a
given day follows a binomial distribution, compute the probability that there will be less than 25
or more than 30 computers that require repair on a given day using a normal approximation.
(Short Answer)
4.7/5  (41)
(41)
The Commissioner of Health in New York State wanted to study malpractice litigation in New
York. A sample of 31 thousand medical records was drawn from a population of 2.7 million
patients who were discharged during 2010. Using the information obtained from the sample to
predict population characteristics with respect to malpractice litigation is an example of _______.
(Short Answer)
4.7/5  (33)
(33)
SCENARIO 9-11
An appliance manufacturer claims to have developed a compact microwave oven that consumes a
population mean of no more than 250 W. From previous studies, it is believed that power
consumption for microwave ovens is normally distributed with a population standard deviation of 15
W. If there is evidence that the population mean consumption is greater than 250 W, the manufacturer
will be unable to make the claim.
-Referring to Scenario 9-11, if you select a sample of 20 compact microwave ovens and are
willing to have a level of significance of 0.01, the probability of making a Type II error is _____
if the mean power consumption of all such microwave ovens is in fact 257.3 W.
(Short Answer)
4.8/5  (29)
(29)
To determine the probability of getting between 2 and 4 events of interest in a
binomial distribution, you will find the area under the normal curve between X = 1.5 and 4.5.
(True/False)
4.8/5  (40)
(40)
SCENARIO 5-11
There are two houses with almost identical characteristics available for investment in two different
neighborhoods with drastically different demographic composition. The anticipated gain in value
when the houses are sold in 10 years has the following probability distribution:  -Referring to Scenario 5-11, what is the total standard deviation of value gain if you invest in both
houses?
-Referring to Scenario 5-11, what is the total standard deviation of value gain if you invest in both
houses?
(Short Answer)
4.9/5  (38)
(38)
Let X represent the amount of time till the next student will arrive in the library parking lot at the university. If we know that the distribution of arrival time can be modeled using an exponential
Distribution with a mean of 4 minutes (i.e. the mean number of arrivals is 1/4 per minute), find
The probability that it will take between 2 and 12 minutes for the next student to arrive at the
Library parking lot.
(Multiple Choice)
4.8/5  (35)
(35)
SCENARIO 11-11
An agronomist wants to compare the crop yield of 3 varieties of chickpea seeds. She plants all 3
varieties of the seeds on each of 5 different patches of fields. She then measures the crop yield in
bushels per acre. Treating this as a randomized block design, the results are presented in the table that
follows. 1 11.1 19.0 14.6 2 13.5 18.0 15.7 3 15.3 19.8 16.8 4 14.6 19.6 16.7 5 9.8 16.6 15.2
-Referring to Scenario 11-11, the agronomist decided to compare the 3 treatment means by using
the Tukey multiple comparison procedure with an overall level of significance of 0.01. How
many pairwise comparisons can be made?
(Short Answer)
4.9/5  (43)
(43)
Showing 401 - 420 of 421
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)