Exam 20: Probability and Combinatorics

SCENARIO 16-16 Given below are the average prices for three types of energy products for five consecutive years. Year Electricity Natural Gas Fuel Oil 1 43.205 25.893 0.892 2 16.959 28.749 0.969 3 47.202 28.933 1.034 4 48.874 29.872 0.913 5 48.693 28.384 0.983 -Referring to Scenario 16-16, what is the Paasche price index for the group of three energy items in year 5 for a family that consumed 13 units of electricity, 26 units of natural gas and 235 units of fuel oil in year 5 using year 1 as the base year?

SCENARIO 16-17 Given below are the prices of a basket of four food items from 2008 to 2012. Year Wheat( \/ Bushel) Corn( \/ Bushel) Soybeans( \/ Bushel) Milk( \/ hundredweight) 2008 4.25 3.71 7.41 15.03 2009 3.43 2.7 7.55 13.63 2010 2.63 2.3 6.05 15.18 2011 2.11 1.97 4.68 14.72 2012 2.16 1.9 4.81 12.32 -Referring to Scenario 16-17, what are the simple price indices for wheat, corn, soybeans and milk, respectively, in 2010 using 2012 as the base year?

SCENARIO 9-14 An appliance manufacturer claims to have developed a compact microwave oven that consumes a population mean of no more than 250 W. From previous studies, it is believed that power consumption for microwave ovens is normally distributed with a population standard deviation of 15 W. If there is evidence that the population mean consumption is greater than 250 W, the manufacturer will be unable to make the claim. -Referring to Scenario 9-14, if you select a sample of 20 compact microwave ovens and are willing to have a level of significance of 0.01, the power of the test is _____ if the mean power consumption of all such microwave ovens is in fact 257.3 W.

The interval between patients arriving at an outpatient clinic follows an exponential distribution at a rate of 15 patients per hour. What is the probability that a randomly chosen arrival to be between 5 minutes and 15 minutes?

SCENARIO 11-11 An agronomist wants to compare the crop yield of 3 varieties of chickpea seeds. She plants all 3 varieties of the seeds on each of 5 different patches of fields. She then measures the crop yield in bushels per acre. Treating this as a randomized block design, the results are presented in the table that follows. 1 11.1 19.0 14.6 2 13.5 18.0 15.7 3 15.3 19.8 16.8 4 14.6 19.6 16.7 5 9.8 16.6 15.2 -Referring to Scenario 11-11, what is the estimated relative efficiency?

SCENARIO 5-11 There are two houses with almost identical characteristics available for investment in two different neighborhoods with drastically different demographic composition. The anticipated gain in value when the houses are sold in 10 years has the following probability distribution: 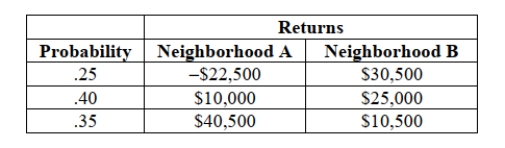-Referring to Scenario 5-11, if you can invest half of your money on the house in neighborhood A and the remaining on the house in neighborhood B, what is the portfolio expected return of your investment?

SCENARIO 11-11 An agronomist wants to compare the crop yield of 3 varieties of chickpea seeds. She plants all 3 varieties of the seeds on each of 5 different patches of fields. She then measures the crop yield in bushels per acre. Treating this as a randomized block design, the results are presented in the table that follows. 1 11.1 19.0 14.6 2 13.5 18.0 15.7 3 15.3 19.8 16.8 4 14.6 19.6 16.7 5 9.8 16.6 15.2 -Referring to Scenario 11-11, the null hypothesis for the randomized block F test for the difference in the means is a) $H _ { 0 } : \mu _ { \text {.Field } 1 } = \mu _ { \text {.Field } 2 } = \mu _ { \text {.Field } 3 } = \mu _ { \text {.Field } 4 } = \mu _ { \text {.Field } 5 }$ b) $H _ { 0 } : \mu _ { \text {.Smith } } = \mu _ { \text {.Walsh } } = \mu _ { \text {.Trevor } }$ c) $H _ { 0 } : M _ { \text {.Field 1 } } = M _ { \text {.Field } 2 } = M _ { \text {.Field } 3 } = M _ { \text {.Field } 4 } = M _ { \text {.Field } 5 }$ d) $\quad H _ { 0 } : M _ { \text {.Smith } } = M _ { \text {.Walsh } } = M _ { \text {.Trevor } }$

SCENARIO 8-14 The president of a university is concerned that the percentage of students who have cheated on an exam is higher than the 1% acceptable level. A confidential random sample of 1,000 students from a population of 7,000 revealed that 6 of them said that they had cheated on an exam during the last semester. -Referring to Scenario 8-14, what is the critical value for the 90% one-sided confidence interval for the proportion of students who had cheated on an exam during the last 12 months?

SCENARIO 6-8 A company has 125 personal computers. The probability that any one of them will require repair on a given day is 0.15. -Referring to Scenario 6-8 and assuming that the number of computers that requires repair on a given day follows a binomial distribution, compute the probability that there will be exactly 10 computers that require repair on a given day using a normal approximation.

SCENARIO 5-14 An accounting firm in a college town usually recruits employees from two of the universities in town. This year, there are fifteen graduates from University A and five from University B and the firm decides to hire six new employees from the two universities. -Referring to Scenario 5-14, what is the probability that two of the new employees will be from University A?

The V in the DCOVA framework stands for "analyze".

SCENARIO 11-11 An agronomist wants to compare the crop yield of 3 varieties of chickpea seeds. She plants all 3 varieties of the seeds on each of 5 different patches of fields. She then measures the crop yield in bushels per acre. Treating this as a randomized block design, the results are presented in the table that follows. 1 11.1 19.0 14.6 2 13.5 18.0 15.7 3 15.3 19.8 16.8 4 14.6 19.6 16.7 5 9.8 16.6 15.2 -Referring to Scenario 11-11, what are the degrees of freedom of the randomized block F test for the difference in the means at a level of significance of 0.01?

SCENARIO 12-21 A filling machine at a local soft drinks company is calibrated to fill the cans at a mean amount of 12 fluid ounces and a standard deviation of 0.5 ounces. The company wants to test whether the standard deviation of the amount filled by the machine is 0.5 ounces. A random sample of 15 cans filled by the machine reveals a standard deviation of 0.67 ounces. -Referring to Scenario 12-21, there is sufficient evidence to conclude that the standard deviation of the amount filled by the machine is not exactly 0.5 ounces when using a 10% level of significance.

To test whether one proportion is higher than the other in two related samples, you can use the McNemar test.

SCENARIO 8-12 The superintendent of a unified school district of a small town wants to make sure that no more than 5% of the students skip more than 10 days of school in a year. A random sample of 145 students from a population of 800 showed that 12 students skipped more than 10 days of school last year. -Referring to Scenario 8-12, what is the critical value for the 95% one-sided confidence interval for the proportion of students who skipped more than 10 days of school last year?

SCENARIO 11-13 An important factor in selecting database software is the time required for a user to learn how to use the system. To evaluate three potential brands (A, B and C) of database software, a company designed a test involving five different employees. To reduce variability due to differences among employees, each of the five employees is trained on each of the three different brands. The amount of time (in hours) needed to learn each of the three different brands is given below: Software Operator A B C 1 17 17 23 2 18 17 23 3 14 13 19 4 12 11 18 5 19 17 22 Mean 16 15 21 $\text { Below is the Excel output for the randomized block design: }$ Source of Variation SS df MS F P-value Fcrit Rows 84.66667 4 21.16667 50.8 9.98-06 3.837853 Columns 103.3333 2 51.66667 124 9.54-07 4.45897 Error 3.333333 8 0.416667 Total 191.3333 14 -Referring to Scenario 11-13, the null hypothesis for the F test for the block effects should be rejected at a 0.05 level of significance.

SCENARIO 8-14 The president of a university is concerned that the percentage of students who have cheated on an exam is higher than the 1% acceptable level. A confidential random sample of 1,000 students from a population of 7,000 revealed that 6 of them said that they had cheated on an exam during the last semester. -Referring to Scenario 8-14, what is the upper bound of the 90% one-sided confidence interval for the proportion of students who had cheated on an exam during the last 12 months?

Unweighted aggregate price indices account for differences in the magnitude of prices per unit and differences in the consumption levels of the items in the market basket.

SCENARIO 8-16 A random sample of 100 stores from a large chain of 500 garden supply stores was selected to determine the mean number of lawnmowers sold at an end-of-season clearance sale. The sample results indicated a mean of 6 and a standard deviation of 2 lawnmowers sold. A 95% confidence interval (5.623 to 6.377) was established based on these results. -Referring to Scenario 8-16, of all possible samples of 100 stores taken from the population of 1,000 stores, 95% of the confidence intervals developed will contain the true population mean within the interval.

A company has 2 machines that produce widgets. An older machine produces 23% defective widgets, while the new machine produces only 8% defective widgets. In addition, the new Machine produces 3 times as many widgets as the older machine does. Given a randomly chosen Widget was tested and found to be defective, what is the probability it was produced by the new Machine?