Exam 4: Introduction to Probability

If a single die is rolled (a cube where the sides are numbered 1 through 6), the probability of rolling at least a 3 is 0.33.

Assume P(A) = 0.6, P(B) = 0.7, and P(A and B) = 0.42, which means that events A and B are independent of each other.

Three events occur with probabilities P(E1) = 0.35, P(E2) = 0.15, P(E3) = 0.40. If the event B occurs, the probability becomes P(E1|B) = 0.25, P(B) = 0.30. Compute P(E1 or B)

When a pair of dice are rolled, the outcome for each die can be said to be:

The managers of a local golf course have recently conducted a study of the types of golf balls used by golfers based on handicap. A joint frequency table for the 100 golfers covered in the survey is shown below: 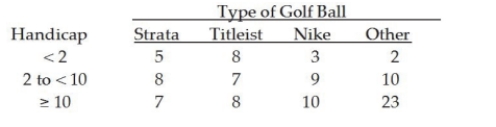Based on these data, the probability of a golfer having a handicap less than 10 is:

There are three general locations that a taxi can go to: the airport, downtown, and elsewhere. When a taxi driver starts in the downtown location, there is a 0.40 chance that his first call will take him to the airport and a 0.40 chance of going to another downtown location. Once a taxi is at the airport, there is a 0.80 probability that the next fare will take him downtown and a 0.20 chance of going elsewhere. The probability of a call from anywhere except downtown taking him to the airport is 0.20. Therefore, the probability that the taxi is at the airport when the third call arrives after going on shift is 0.20.

It is correct to say that subjective probability assessments are neither right nor wrong, but are merely reflections of the state of mind of the individual making the probability assessment.

When the salesperson makes a sale, there are three possible sales levels: large, medium, and small. The probability of a large sale is 0.20 and the chance of a medium sale is 0.60. If a salesperson makes two sales, the probability that at least one is large is 0.36.

Three events occur with probabilities P(E1) = 0.35, P(E2) = 0.15, P(E3) = 0.40. If the event B occurs, the probability becomes P(E1|B) = 0.25, P(B) = 0.30. Calculate P(E1 and B)

The Jack In The Box franchise in Bangor, Maine, has determined that the chance a customer will order a soft drink is 0.90. The probability that a customer will order a hamburger is 0.60. The probability that a customer will order french fries is 0.50. The restaurant has also determined that if a customer orders a hamburger, the probability the customer will also order fries is 0.80. Determine the probability that the order will include a hamburger and fries.

In most situations, there is no difference between the events and the elementary events.

The managers of a local golf course have recently conducted a study of the types of golf balls used by golfers based on handicap. A joint frequency table for the 100 golfers covered in the survey is shown below: 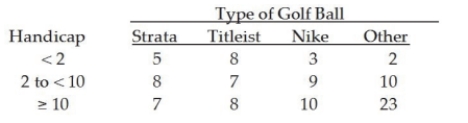Based on these data, the probability of someone using a Strata ball and having a handicap under 2 is:

Until the summer of 2006, the real estate market in Fresno, California, had been booming, with prices skyrocketing. Recently, a study showed the sales patterns in Fresno for single-family homes. One chart presented in the commission's report is reproduced here. It shows the number of homes sold by price range and number of days the home was on the market. 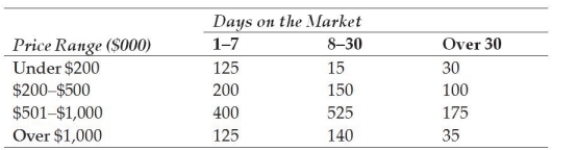Using the relative frequency approach to probability assessment, what is the probability that a house will be on the market more than 7 days?

The Vintage Clothing Company has three retail locations, code-named A, B, and C. The following table illustrates the percentage of total company sales at each store and also the percentage of customers at that store who make purchases with credit cards: Based on this information, the probability that a customer will use a credit card is just slightly greater than 0.55.

Parts and Materials for the skis made by the Downhill Adventures Company are supplied by two suppliers. Supplier A's materials make up 30% of what is used, with supplier B providing the rest. Past records indicate that 15% of supplier A's materials are defective and 10% of B's are defective. Since it is impossible to tell which supplier the materials came from once they are in inventory, the manager wants to know which supplier most likely supplied the defective materials the foreman has brought to his attention. Provide the manager this information.

The managers of a local golf course have recently conducted a study of the types of golf balls used by golfers based on handicap. A joint frequency table for the 100 golfers covered in the survey is shown below: 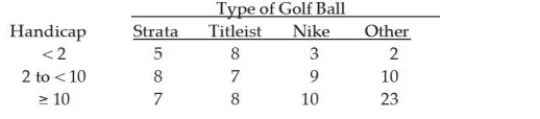If a player comes to the course using a Nike golf ball, the probability that he or she has a handicap of at least 10 is:

The following probability distribution was subjectively assessed for the number of sales a salesperson would make if he or she made five sales calls in one day. 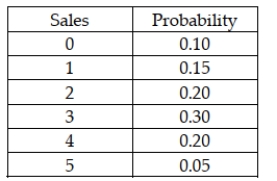Given this distribution, the probability that the number of sales is 2 or 3 is 0.50.

When the salesperson makes a sale, there are three possible sales levels: large, medium, and small. The probability of a large sale is 0.20 and the chance of a medium sale is 0.60. Thus, when a sale is made, the chance of it being a small sale is 0.20.

An inventory of appliances contains four white washers and one black washer. If a customer selects one at random, what is the probability that the black washer will be selected?

A car salesman states that the probability that the dealership sells a car on a Saturday morning is .30. The method of probability assessment that he has used is most likely classical assessment.