Exam 7: Introduction to Sampling Distributions

If you are sampling from a very large population, a doubling of the sample size will reduce the standard error of the sampling distribution by one-fourth.

One of the nation's biggest regional airlines has tracked 4,000 landings and take-offs during the past month. Treating these data as the population of interest, the company found that the average time the planes spent on the ground (called the turn time) was 17.23 minutes with a standard deviation of 3.79 minutes. Further, they determined that the distribution of turn times is normally distributed. If a sample of size n = 16 turn times was selected at random from the population, the chances of the mean of this sample exceeding 20 minutes is 0.2327.

A particular subdivision has 20 homes. The number of people living in each of these homes is listed as follows: 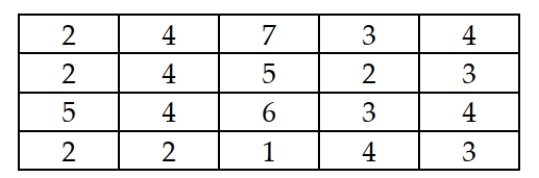If a sample of size n = 5 is selected, the largest possible sample mean is:

In a recent report, it was stated that the proportion of employees who carpool to their work is 0.14 and that the standard deviation of the sampling proportion is 0.0259. However, the report did not indicate what the sample size was. What was the sample size?

SeeClear Windows makes windows for use in homes and commercial buildings. The standards for glass thickness call for the glass to average 0.375 inches with a standard deviation equal to 0.050 inch. Suppose a random sample of n = 50 windows yields a sample mean of 0.392 inches. What is the probability if the windows meet the standards?

The proportion of items in a population that possess a specific attribute is known to be 0.70. If a simple random sample of size n = 100 is selected and the proportion of items in the sample that contain the attribute of interest is 0.65, what is the sampling error?

A measure computed from the entire population is called:

A larger sample size reduces the potential for large sampling error.

The Olsen Agricultural Company has determined that the weight of hay bales is normally distributed with a mean equal to 80 pounds and a standard deviation equal to 8 pounds. Based on this, what is the mean of the sampling distribution for if the sample size is n = 64?

A major textbook publisher has a contract with a printing company. Part of the contract stipulates that no more than 5 percent of the pages should have any type of printing error. Suppose that the company selects a random sample of 400 pages and finds 33 that have an error. If the printer is meeting the standard, what is the probability that a sample would have 33 or more errors?

A smaller sample might provide less sampling error than a larger sample from a given population.

Recently the State Fish and Game planted several thousand tagged fish in a local river. The mean length of these fish, which constitute a population, is 12.6 inches. Yesterday, fishermen caught 100 of these tagged fish. You could expect that the mean length for these fish would be 12.6 inches as well since they come from the population.

The population of soft drink cans filled by a particular machine is known to be normally distributed with a mean equal to 12 ounces and a standard deviation equal to .25 ounce. Given this information, the sampling distribution for a random sample of n = 25 cans will also be normally distributed with a mean equal to 12 ounces and a standard deviation equal to .05 ounce.

A simple random sample is selected in a manner such that each possible sample of a given size has an equal chance of being selected.

Hillman Management Services manages apartment complexes in Tulsa, Oklahoma. They currently have 30 units available for rent. The monthly rental prices (in dollars) for this population of 30 units are: What is the range of possible sampling error if a random sample of size n = 10 is selected?

It is very unlikely that a nonstatistical sample will ever provide less sampling error than a statistical sample of the same size.

Suppose it is known that 93 percent of all parts in an inventory of 18,900 parts are in workable order. If a sample of n = 100 parts were selected from the inventory, based on the concept of sampling distributions of proportions, it can be assumed that the sample proportion of workable parts will also be 0.93.

The following values represent the population of home mortgage interest rates (in percents) being charged by the banks in a particular city: Given this information, what is the smallest to largest range for the sampling error possible if a random sample of n = 3 banks is surveyed and the mean loan rate is calculated?

The J.R. Simplot Company produces frozen French fries that are then sold to customers such as McDonald's. The "prime" line of fries has an average length of 6.00 inches with a standard deviation of 0.50 inch. To make sure that Simplot continues to meet the quality standard for "prime" fries, they plan to select a random sample of n = 100 fries each day. The quality analysts will compute the mean length for the sample. They want to establish limits on either side of the 6.00 inch mean so that the chance of the sample mean falling within the limits is 0.99. What should these limits be?

The J R Simplot Company is one of the world's largest privately held agricultural companies, employing over 10,000 people in the United States, Canada, China, Mexico, and Australia. More information can be found at the company's Web site: www.Simplot.com. One of its major products is french fries that are sold primarily on the commercial market to customers such as McDonald's and Burger King. French fries have numerous quality attributes that are important to customers. One of these is called "dark ends," which are the dark-colored ends that can occur when the fries are cooked. Suppose a major customer will accept no more than 0.06 of the fries having dark ends. Recently, the customer called the Simplot Company saying that a recent random sample of 300 fries was tested from a shipment and 27 fries had dark ends. Assuming that the population does meet the 0.06 standard, what is the probability of getting a sample of 300 with 27 or more dark ends?