Exam 8: Estimating Single Population Parameters

A statement in the newspaper attributed to the leader of a local union stated that the average hourly wage for union members in the region is $13.35. He indicated that this number came from a survey of union members. If an estimate was developed with 95 percent confidence, we can safely conclude that this value is within 95 percent of the true population mean hourly wage.

The procurement manager for a large company wishes to estimate the proportion of parts from a supplier that are defective. She has selected a random sample of n = 200 incoming parts and has found 11 to be defective. Based on a 95 percent confidence level, the upper and lower limits for the confidence interval estimate are approximately 0.0234 to 0.0866.

The national sales manager for a textbook publishing company wishes to estimate the mean number of books sold per college. She wishes to have her estimate be within ± 30 copies and wants a 95 percent confidence interval estimate. If a pilot sample of 30 schools gave a sample standard deviation equal to 60 books, the required total sample size is less than the pilot sample already taken.

The bottlers of a new fruit juice daily select a random sample of 12 bottles of the drink to estimate the mean quantity of juice in the bottles filled that day. On one such day, the following results were observed: 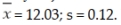Based on this information, the upper limit for a 95 percent confidence interval estimate is approximately 12.106 ounces.

A report in a consumer magazine indicated that with 90 percent confidence, the mean number of hours that a particular brand light bulb lasts is between 900 and 1,100 hours. Based on this, the sample mean that produced this estimate is 1,000 hours.

The State Transportation Department wishes to estimate the mean speed of vehicles on a certain stretch of highway. They wish to estimate the mean within ±0.75 mph and they wish to have a confidence level equal to 99 percent. Based on this information only, they can determine that the required sample size is 320 vehicles.

A cell phone service provider has selected a random sample of 20 of its customers in an effort to estimate the mean number of minutes used per day. The results of the sample included a sample mean of 34.5 minutes and a sample standard deviation equal to 11.5 minutes. Based on this information, and using a 95 percent confidence level:

When determining sample size for a proportion, the farther that p is from 0.5, the smaller the resulting sample size will be.

In an application to estimate the mean number of miles that downtown employees commute to work roundtrip each day, the following information is given: 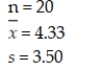If the desired confidence level is 95 percent, the appropriate critical value is:

A hospital emergency room has collected a sample of n = 40 to estimate the mean number of visits per day. It has found the standard deviation is 32. Using a 90 percent confidence level, what is its margin of error?

When determining sample size for a proportion, using p = 0.5 will produce the smallest possible value for n.

An advertising company wishes to estimate the mean household income for all single working professionals who own a foreign automobile. If the advertising company wants a 90% confidence interval estimate with a margin of error of ±$2,500, what sample size is needed if the population standard deviation is known to be $27,500?

For a given sample size and a given confidence level, the closer p is to 1.0, the greater the margin of error will be.

What are the disadvantages of using a small sample to estimate the population mean?

The produce manager for a large retail food chain is interested in estimating the percentage of potatoes that arrive on a shipment with bruises. A random sample of 150 potatoes showed 14 with bruises. Based on this information, what is the margin of error for a 95 percent confidence interval estimate?

The concept of margin of error applies directly when estimating a population mean, but is not appropriate when estimating a population proportion.

A financial analyst is interested in estimating the proportion of publicly traded companies on the New York Stock Exchange that have cash balances that are more than 10 percent of the total assets of the company. A random sample of n = 100 companies shows that 13 had cash balances of more than 10 percent of assets. Based on this information, develop and interpret a 90 percent confidence interval estimate for the population proportion.

In an effort to estimate the mean length of stay for motel guests at a major national motel chain, the decision makers asked for a 95 percent confidence, and a margin of error of ±0.25 days. Further, it was known that the population standard deviation is 0.50 days. Given this, the required sample size to estimate the mean length of stay is about 16 customers.

In a recent report to the supply-chain manager in a major electronics company, the report writer stated that with 90 percent confidence, the manufacturing lead time for a critical part is between 3.34 hours and 4.14 hours. Based on this information, the margin of error for this estimate is ±.80 hours.

If a manager is interested in estimating the mean time customers spend shopping in a store on each visit to the store, she may want to develop a confidence interval estimate. Suppose, she has determined the required sample size and feels that she cannot afford one that large. What options are available?