Exam 2: A: Basic Structures: Sets, Functions, Sequences, Sums, Matrices
Exam 1: The Foundations: Logic and Proofs18 Questions
Exam 1: A: the Foundations: Logic and Proofs201 Questions
Exam 2: Basic Structures: Sets, Functions, Sequences, Sums, Matrices5 Questions
Exam 2: A: Basic Structures: Sets, Functions, Sequences, Sums, Matrices210 Questions
Exam 3: Algorithms8 Questions
Exam 3: A: Algorithms54 Questions
Exam 4: Number Theory and Cryptography10 Questions
Exam 4: A: Number Theory and Cryptography149 Questions
Exam 5: Induction and Recursion10 Questions
Exam 5: A: Induction and Recursion51 Questions
Exam 6: Counting14 Questions
Exam 6: A: Counting155 Questions
Exam 7: Discrete Probability9 Questions
Exam 7: A: Discrete Probability50 Questions
Exam 8: Advanced Counting Techniques16 Questions
Exam 8: A: Advanced Counting Techniques124 Questions
Exam 9: Relations13 Questions
Exam 9: A: Relations72 Questions
Exam 10: Graphs14 Questions
Exam 10: A: Graphs131 Questions
Exam 11: Trees13 Questions
Exam 11: A: Trees94 Questions
Exam 12: Boolean Algebra11 Questions
Exam 12: A: Boolean Algebra67 Questions
Exam 13: Modeling Computation14 Questions
Exam 13: A: Modeling Computation67 Questions
Exam 14: Mathematics Problem Set: Set Theory, Number Theory, Combinatorics, and Boolean Algebra29 Questions
Select questions type
mark each statement TRUE or FALSE. Assume that the statement applies to all sets.
-
(True/False)
4.9/5  (29)
(29)
determine whether the set is finite or infinite. If the set is finite, find its size.
-{1, 10, 100, 1000, . . .}
(Short Answer)
4.9/5  (34)
(34)
describe each sequence recursively. Include initial conditions and assume that the sequences begin with .
-an = 1 + 2 + 3 + · · · + n
(Short Answer)
4.7/5  (36)
(36)
Suppose A = and C = . Find a matrix B such that AB = C or prove that no such matrix exists.
(Short Answer)
4.7/5  (35)
(35)
suppose the following are fuzzy sets: F=\{0.7 Ann ,0.1 Bill ,0.8 Fran ,0.3 Olive ,0.5 Tom \}, R=\{0.4 Ann ,0.9 Bill ,0.9 Fran ,0.6 Olive ,0.7 Tom \}
-
(Short Answer)
4.9/5  (37)
(37)
find the inverse of the function f or else explain why the function has no inverse.
-
(Short Answer)
4.8/5  (38)
(38)
Suppose B = and C = . Find a matrix A such that AB= C or prove that no such matrix exists.
(Short Answer)
4.8/5  (33)
(33)
determine whether the set is finite or infinite. If the set is finite, find its size.
-
(Short Answer)
4.8/5  (30)
(30)
Suppose f : Z → Z has the rule f(n) = 3n − 1. Determine whether f is onto Z.
(Short Answer)
4.7/5  (34)
(34)
determine whether the rule describes a function with the given domain and codomain.
-
(Short Answer)
4.9/5  (35)
(35)
suppose g: A → B and f : B → C where A = {1, 2, 3, 4}, B = {a, b, c}, C = {2, 8, 10}, and g and f are defined by g = f(1, b), (2, a), (3, b), (4, a)g and f = {(a, 8), (b, 10); (c, 2)}.
-
(Short Answer)
4.8/5  (37)
(37)
suppose A = {a, b, c} and B = {b, {c}}. Mark the statement TRUE or FALSE.
-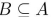
(True/False)
4.9/5  (35)
(35)
determine whether the given set is the power set of some set. If the set is a power set, give the set of which it is a power set.
-
(Short Answer)
4.8/5  (43)
(43)
mark each statement TRUE or FALSE. Assume that the statement applies to all sets.
-(A − C) − (B − C) = A − B
(True/False)
4.9/5  (33)
(33)
Showing 61 - 80 of 210
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)