Exam 3: A: Algorithms

Prove that $\frac { x ^ { 3 } + 7 x ^ { 2 } + 3 } { 2 x + 1 } \text { is } \Theta \left( x ^ { 2 } \right) \text {. }$

find the best big-O function for the function. Choose your answer from among the following: $\text { 1, } \log _ { 2 } n , n , n \log _ { 2 } n , n ^ { 2 } , n ^ { 3 } , \ldots , 2 ^ { n } , n !$ - $[ n + 2 ] \cdot [ n / 3 \rceil$

Use the definition of big-O to prove that $\frac { 6 n + 4 n ^ { 5 } - 4 } { 7 n ^ { 2 } - 3 } \text { is } O \left( n ^ { 3 } \right)$

Arrange the following functions in a list so each is big-O of the next one in the list: $\log n ^ { 2 } , \log \log n , n \log n$ $\log \left( n ^ { 2 } + 1 \right) , \log 2 ^ { n }$

Arrange the following functions in a list so each is big-O of the next one in the list: $n ^ { 3 } + 88 n ^ { 2 } + 3 , \log n ^ { 4 }$ $3 ^ { n } , n ^ { 2 } \log n , n \cdot 2 ^ { n } , 10000$

Describe an algorithm that takes a list of integers a₁, a₂, . . . , a_n 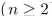and finds the second-largest integer in the sequence by going through the list and keeping track of the largest and second-largest integer encountered.

find the best big-O function for the function. Choose your answer from among the following: $\text { 1, } \log _ { 2 } n , n , n \log _ { 2 } n , n ^ { 2 } , n ^ { 3 } , \ldots , 2 ^ { n } , n !$ - $f ( n ) = 1 + 2 + 3 + \cdots + \left( n ^ { 2 } - 1 \right) + n ^ { 2 }$

find the "best" big-O notation to describe the complexity of the algorithm. Choose your answers from the following: $1 , \log _ { 2 } n , n , n \log _ { 2 } n , n ^ { 2 } , n ^ { 3 } , \ldots , 2 ^ { n } , n !$ -A linear search to find the smallest number in a list of n numbers.

find the "best" big-O notation to describe the complexity of the algorithm. Choose your answers from the following: $1 , \log _ { 2 } n , n , n \log _ { 2 } n , n ^ { 2 } , n ^ { 3 } , \ldots , 2 ^ { n } , n !$ -An algorithm that lists all ways to put the numbers 1, 2, 3, . . . , n in a row.

Describe in words how the binary search works.

find the best big-O function for the function. Choose your answer from among the following: $\text { 1, } \log _ { 2 } n , n , n \log _ { 2 } n , n ^ { 2 } , n ^ { 3 } , \ldots , 2 ^ { n } , n !$ - $3 n ^ { 4 } + \log _ { 2 } n ^ { 8 }$

Express a brute-force algorithm that finds the second largest element in a list a₁, a₂, . . . , a_n $( n \geq 2 )$ of distinct integers by finding the largest element, placing it at the beginning of the sequence, then finding the largest element of the remaining sequence.

find the "best" big-O notation to describe the complexity of the algorithm. Choose your answers from the following: $1 , \log _ { 2 } n , n , n \log _ { 2 } n , n ^ { 2 } , n ^ { 3 } , \ldots , 2 ^ { n } , n !$ -The number of print statements in the following:

Find the best big-O function for $n ^ { 3 } + \sin n ^ { 7 }$

Find the best big-O function for $\frac { x ^ { 3 } + 7 x } { 3 x + 1 }$

Show that $f ( x ) = ( x + 2 ) \log _ { 2 } \left( x ^ { 2 } + 1 \right) + \log _ { 2 } \left( x ^ { 3 } + 1 \right) \text { is } O \left( x \log _ { 2 } x \right)$

Find all pairs of functions in this list that are of the same order: $n ^ { 2 } + \log n , 2 ^ { n } + 3 ^ { n } , 100 n ^ { 3 } + n ^ { 2 } , n ^ { 2 } + 2 ^ { n }$ $n ^ { 2 } + n ^ { 3 } , 3 n ^ { 3 } + 2 ^ { n }$

Prove or disprove that the cashier's algorithm for making change always uses the fewest coins possible when the denominations available are pennies (1-cent coins), nickels (5-cent coins), and quarters (25-cent coins).

find the best big-O function for the function. Choose your answer from among the following: $\text { 1, } \log _ { 2 } n , n , n \log _ { 2 } n , n ^ { 2 } , n ^ { 3 } , \ldots , 2 ^ { n } , n !$ - $g ( n ) = 1 + 3 + 5 + 7 + \cdots + ( 2 n - 1 )$

assume that the number of multiplications of entries used to multiply a p × q and a q × r matrix is pqr. -What is the most efficient way to multiply the matrices A₁, A₂, A₃ of sizes 20 × 5, 5 × 50, 50 × 5?