Exam 3: A: Algorithms
Exam 1: The Foundations: Logic and Proofs18 Questions
Exam 1: A: the Foundations: Logic and Proofs201 Questions
Exam 2: Basic Structures: Sets, Functions, Sequences, Sums, Matrices5 Questions
Exam 2: A: Basic Structures: Sets, Functions, Sequences, Sums, Matrices210 Questions
Exam 3: Algorithms8 Questions
Exam 3: A: Algorithms54 Questions
Exam 4: Number Theory and Cryptography10 Questions
Exam 4: A: Number Theory and Cryptography149 Questions
Exam 5: Induction and Recursion10 Questions
Exam 5: A: Induction and Recursion51 Questions
Exam 6: Counting14 Questions
Exam 6: A: Counting155 Questions
Exam 7: Discrete Probability9 Questions
Exam 7: A: Discrete Probability50 Questions
Exam 8: Advanced Counting Techniques16 Questions
Exam 8: A: Advanced Counting Techniques124 Questions
Exam 9: Relations13 Questions
Exam 9: A: Relations72 Questions
Exam 10: Graphs14 Questions
Exam 10: A: Graphs131 Questions
Exam 11: Trees13 Questions
Exam 11: A: Trees94 Questions
Exam 12: Boolean Algebra11 Questions
Exam 12: A: Boolean Algebra67 Questions
Exam 13: Modeling Computation14 Questions
Exam 13: A: Modeling Computation67 Questions
Exam 14: Mathematics Problem Set: Set Theory, Number Theory, Combinatorics, and Boolean Algebra29 Questions
Select questions type
You have supplies of boards that are one foot, five feet, seven feet, and twelve feet long. You need to lay pieces end-to-end to make a molding 15 feet long and wish to do this using the fewest number of pieces possible. Explain why the greedy algorithm of taking boards of the longest length at each stage (so long as the total length of the boards selected does not exceed 15 feet) does not give the fewest number of boards possible.
(Essay)
4.9/5  (32)
(32)
Describe an algorithm that takes a list of n integers and finds the location of the last even integer in the list, and returns 0 if there are no even integers in the list.
(Essay)
4.8/5  (36)
(36)
find the "best" big-O notation to describe the complexity of the algorithm. Choose your answers from the following:
-The best-case analysis of a linear search of a list of size n (counting the number of comparisons)
(Short Answer)
4.8/5  (40)
(40)
find the "best" big-O notation to describe the complexity of the algorithm. Choose your answers from the following:
-An algorithm that prints all subsets of size three of the set {1, 2, 3, . . . , n}
(Short Answer)
4.8/5  (32)
(32)
Express a brute-force algorithm that finds the largest product of two numbers in a list a1, a2, . . . , an (n ≥ 2) that is less than a threshold N .
(Essay)
4.8/5  (36)
(36)
Prove or disprove that the cashier's algorithm for making change always uses the fewest coins possible when the denominations available are 1-cent coins, 8-cent coins, and 20-cent coins.
(True/False)
4.8/5  (34)
(34)
Give a big-O estimate for the number of operations (where an operation is an addition or a multiplication) used in this segment of an algorithm:
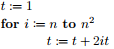
(Short Answer)
4.7/5  (36)
(36)
find the "best" big-O notation to describe the complexity of the algorithm. Choose your answers from the following:
-A binary search of n elements.
(Short Answer)
4.9/5  (41)
(41)
find the best big-O function for the function. Choose your answer from among the following:
-
(Short Answer)
4.8/5  (27)
(27)
assume that the number of multiplications of entries used to multiply a p × q and a q × r matrix is pqr.
-What is the best order to form the product ABC if A, B and C are matrices with dimensions 8 × 3, 3 × 6 and 6 × 12, respectively?
(Essay)
4.8/5  (23)
(23)
Showing 41 - 54 of 54
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)