Exam 10: A: Graphs
Exam 1: The Foundations: Logic and Proofs18 Questions
Exam 1: A: the Foundations: Logic and Proofs201 Questions
Exam 2: Basic Structures: Sets, Functions, Sequences, Sums, Matrices5 Questions
Exam 2: A: Basic Structures: Sets, Functions, Sequences, Sums, Matrices210 Questions
Exam 3: Algorithms8 Questions
Exam 3: A: Algorithms54 Questions
Exam 4: Number Theory and Cryptography10 Questions
Exam 4: A: Number Theory and Cryptography149 Questions
Exam 5: Induction and Recursion10 Questions
Exam 5: A: Induction and Recursion51 Questions
Exam 6: Counting14 Questions
Exam 6: A: Counting155 Questions
Exam 7: Discrete Probability9 Questions
Exam 7: A: Discrete Probability50 Questions
Exam 8: Advanced Counting Techniques16 Questions
Exam 8: A: Advanced Counting Techniques124 Questions
Exam 9: Relations13 Questions
Exam 9: A: Relations72 Questions
Exam 10: Graphs14 Questions
Exam 10: A: Graphs131 Questions
Exam 11: Trees13 Questions
Exam 11: A: Trees94 Questions
Exam 12: Boolean Algebra11 Questions
Exam 12: A: Boolean Algebra67 Questions
Exam 13: Modeling Computation14 Questions
Exam 13: A: Modeling Computation67 Questions
Exam 14: Mathematics Problem Set: Set Theory, Number Theory, Combinatorics, and Boolean Algebra29 Questions
Select questions type
How many different channels are needed for six television stations (A, B, C, D, E, F ) whose distances (in miles) from each other are shown in the following table? Assume that two stations cannot use the same channel when they are within 150 miles of each other? A B C D E F A - 85 175 100 50 100 B 85 - 125 175 100 130 C 175 125 - 100 200 250 D 100 175 100 - 210 220 E 50 100 200 210 - 100 F 100 130 250 220 100 -
(Essay)
4.8/5  (42)
(42)
either give an example or prove that there are none.
-A graph with region-chromatic number equal to 6.
(Short Answer)
4.9/5  (25)
(25)
either give an example or prove that there are none.
-A simple digraph with indegrees 0, 1, 1, 2 and outdegrees 0, 1, 1, 1.
(Essay)
4.9/5  (35)
(35)
Give a recurrence relation for en = the number of edges of the graph
(Short Answer)
4.8/5  (39)
(39)
fill in the blanks.
-There are ____ non-isomorphic simple digraphs with 3 vertices and 2 edges.
(Short Answer)
4.8/5  (27)
(27)
The Math Department has 6 committees that meet once a month. How many different meeting times must be used to guarantee that no one is scheduled to be at 2 meetings at the same time, if committees and their members are: Allen, Brooks, Marg Brooks, Jones, Morton Allen, Marg, Morton , Jones, Marg, Morton Allen, Brooks Brooks, Marg, Morton .
(Essay)
4.9/5  (43)
(43)
Draw a cubic graph with 6 vertices that is not isomorphic to K3,3, or else prove that there are none.
(Essay)
4.9/5  (36)
(36)
fill in the blanks.
-The length of the longest simple circuit in is ____.
(Short Answer)
4.9/5  (42)
(42)
Find the vertex-chromatic number, the edge-chromatic number, and the region-chromatic number for W5.
(Essay)
4.8/5  (40)
(40)
Consider the graph at the right. 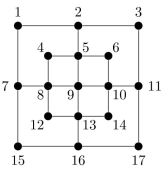 (a) Does it have an Euler circuit?
(b) Does it have an Euler path?
(c) Does it have a Hamilton circuit?
(d) Does it have a Hamilton path?
(a) Does it have an Euler circuit?
(b) Does it have an Euler path?
(c) Does it have a Hamilton circuit?
(d) Does it have a Hamilton path?
(Short Answer)
4.8/5  (33)
(33)
In K3,3 let a and b be any two adjacent vertices. Find the number of paths between a and b of length 3.
(Short Answer)
4.8/5  (34)
(34)
either give an example or prove that there are none.
-A planar graph with 7 vertices, 9 edges, and 5 regions.
(Short Answer)
4.9/5  (31)
(31)
Many supermarkets use loyalty or discount cards to keep track of who buys which items. How can graphs be used to model this relationship? Should the edges be directed or undirected? Should multiple edges be allowed? Should loops be allowed? Does this graph have any special properties?
(Essay)
4.9/5  (33)
(33)
Determine whether the graph is strongly connected, and if not, whether it is weakly connected. 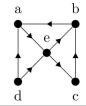
(Essay)
4.9/5  (29)
(29)
Find the vertex-chromatic number, the edge-chromatic number, and the region-chromatic number for Q3.
(Essay)
4.9/5  (35)
(35)
Showing 61 - 80 of 131
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)