Exam 6: Matrices and Determinants

Find the product AB, if possible. - $\mathrm { A } = \left[ \begin{array} { r r } - 1 & 3 \\ 1 & 6 \end{array} \right] , \mathrm { B } = \left[ \begin{array} { l l l } 0 & - 2 & 4 \\ 1 & - 3 & 2 \end{array} \right]$

Write the augmented matrix for the system of equations. - 6x+9y+6z=54 4x+2y+7z=17 3x-2y+2z=2

Find the products AB and BA to determine whether B is the multiplicative inverse of A. - $\mathrm { A } = \left[ \begin{array} { l l l } 1 & 0 & 0 \\1 & 1 & 0 \\1 & 1 & 1\end{array} \right] , \quad \mathrm { B } = \left[ \begin{array} { r r r } 1 & 0 & 0 \\- 1 & 1 & 0 \\0 & - 1 & 1\end{array} \right]$

Use Cramer's rule to solve the system. - 4x-6y-3z=-53 -5x+6y+7z=69 8x-8y+7z=-5

Write the system of linear equations represented by the augmented matrix. Use x, y, z, and, if necessary, w for the variables. Then use back-substitution to find the solution. - $\left[ \begin{array} { r r r r | r } 1 & 1 & - 1 & 1 & - 6 \\ 0 & 1 & - 4 & 8 & 0 \\ 0 & 0 & 1 & 4 & 13 \\ 0 & 0 & 0 & 1 & - 3 \end{array} \right]$

Solve Problems Involving Systems Without Unique Solutions Solve the problem using matrices. -A company that manufactures products A, B, and C does both assembly and testing. The hours needed to assemble and test each product are shown in the table below. The company has exactly 24 hours per week available for assembly and 109 hours per week available for testing. If the company must produce $t$ units of Product $C$ this week, how many units of Products $A$ and $B$ can they produce?

Solve the problem using matrices. -The final grade for an algebra course is determined by grades on the midterm and final exam. The grades for four students and two possible grading systems are modeled by the following matrices. 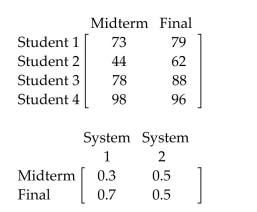Find the final course score for Student 3 for both grading System 1 and System $2 .$

Use Inverses to Solve Matrix Equations Write the linear system as a matrix equation in the form AX = B, where A is the coefficient matrix and B is the constant matrix. - 2x+3z=17 2y+7z=21 2x+5y+5z=54

Encode and Decode Messages Encode or decode the given message, as requested, numbering the letters of the alphabet 1 through 26 in their usual order. -Use the coding matrix $\mathrm { A } = \left[ \begin{array} { r r r } 1 & 1 & 1 \\ - 1 & 1 & 2 \\ 1 & 2 & 3 \end{array} \right]$ and its inverse $\mathrm { A } ^ { - 1 } = \left[ \begin{array} { r r r } - 1 & - 1 & 1 \\ 5 & 2 & - 3 \\ - 3 & - 1 & 2 \end{array} \right]$ to decode the cryptogram $\left[ \begin{array} { l l l } 37 & 16 & 35 \\ 38 & 20 & 4 \\ 82 & 40 & 60 \end{array} \right]$ .

Apply Gaussian Elimination to Systems Without Unique Solutions Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists. - x+y+z+w=8 3x+2y+z+4w=21 4x+4y+5z+8w=30 2x+3y+6z+9w=15

Apply Gaussian Elimination to Systems with More Variables than Equations Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists. - 5x-y+z=8 7x+y+z=6

Apply Gaussian Elimination to Systems Without Unique Solutions Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists. - x+8y+8z =8 7x+7y+z =1 8x+15y+9z =-9

Evaluate the determinant. - $\left| \begin{array} { l l l l } 1 & 7 & 5 & 3 \\4 & 4 & 5 & 5 \\2 & 8 & 0 & 6 \\7 & 5 & 3 & 6\end{array} \right|$

Evaluate the determinant. - $\left| \begin{array} { l l l l } 0 & 0 & 0 & 8 \\3 & 4 & 5 & 8 \\5 & 4 & 7 & 2 \\7 & 2 & 3 & 7\end{array} \right|$

Give the order of the matrix, and identify the given element of the matrix. - $\left[ \begin{array} { c c c c } - 1 & 9 & 5 & 13 \\- 13 & 7 & - 15 & - 10\end{array} \right] ; a _ { 12 }$

Use Cramer's rule to determine if the system is inconsistent system or contains dependent equations. - 4x-y+2z=1 3x+5y-z=0 -6x-10y+2z=0

Solve the system using the inverse that is given for the coefficient matrix. - $x + 2 y + 3 z = 7$ $x + y + z = 6$ $x - 2 z = - 6$ The inverse of $\left[ \begin{array} { r r r } 1 & 2 & 3 \\ 1 & 1 & 1 \\ 1 & 0 & - 2 \end{array} \right]$ is $\left[ \begin{array} { r r r } - 2 & 4 & - 1 \\ 3 & - 5 & 2 \\ - 1 & 2 & - 1 \end{array} \right]$ .

Use Cramer's rule to determine if the system is inconsistent system or contains dependent equations. - 9x+y=32 9x+y=59

Model Applied Situations with Matrix Operations The $\perp$ shape in the figure below is shown using 9 pixels in a $3 \times 3$ grid. The color levels are given to the right of the figure. Use the matrix $\left[ \begin{array} { l l l } 1 & 3 & 1 \\ 1 & 3 & 1 \\ 3 & 3 & 3 \end{array} \right]$ that represents a digital photograph of the $\perp$ shape to solve the problem. -Adjust the contrast by changing the black to dark grey and the light grey to white. Use matrix addition to accomplish this.

Find the products AB and BA to determine whether B is the multiplicative inverse of A. - $A = \left[ \begin{array} { r r } - 3 & - 1 \\ 2 & - 4 \end{array} \right]$