Exam 6: Matrices and Determinants
Exam 1: Equations and Inequalities420 Questions
Exam 2: Functions and Graphs83 Questions
Exam 3: Polynomial and Rational Functions98 Questions
Exam 4: Exponential and Logarithmic Functions268 Questions
Exam 5: Systems of Equations and Inequalities287 Questions
Exam 6: Matrices and Determinants152 Questions
Exam 7: Conic Sections120 Questions
Exam 8: Sequences, Induction, and Probability303 Questions
Select questions type
Use Inverses to Solve Matrix Equations
Write the linear system as a matrix equation in the form AX = B, where A is the coefficient matrix and B is the
constant matrix.
-
(Multiple Choice)
4.9/5  (38)
(38)
Find the products AB and BA to determine whether B is the multiplicative inverse of A.
-
(Multiple Choice)
4.9/5  (38)
(38)
Understand What is Meant by Equal Matrices
Find values for the variables so that the matrices are equal.
-
(Multiple Choice)
4.7/5  (36)
(36)
Solve the problem using matrices.
-State University has a College of Arts & Sciences, a College of Business, and a College of Engineering. The percentage of students in each category are given by the following matrix.  The student population is distributed by class and age as given in the following matrix.
The student population is distributed by class and age as given in the following matrix.
 How many female students are in the College of Business? How many male students are in the College of Arts \& Sciences?
How many female students are in the College of Business? How many male students are in the College of Arts \& Sciences?
(Multiple Choice)
4.8/5  (27)
(27)
Encode and Decode Messages
Encode or decode the given message, as requested, numbering the letters of the alphabet 1 through 26 in their usual
order.
-Use the coding matrix to encode the message COME_HERE.
(Multiple Choice)
4.7/5  (31)
(31)
Solve Problems Involving Systems Without Unique Solutions
Solve the problem using matrices.
-The figure below shows the intersection of three one-way streets. To keep traffic moving, the number of cars per minute entering an intersection must equal the number of cars leaving that intersection. Set up a
System of equations that keeps traffic moving, and use Gaussian elimination to solve the system. If
Construction limits z to t cars per minute, how many cars per minute must pass through the other
Intersections to keep traffic moving? 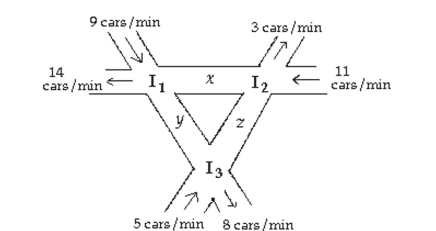
(Multiple Choice)
4.8/5  (35)
(35)
Apply Gaussian Elimination to Systems Without Unique Solutions
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
- x+y+z=7 x-y+2z=7 2x+3z=14
(Multiple Choice)
4.8/5  (33)
(33)
Solve the problem.
-
then the points , and are collinear. If the determinant does not equal 0 , then the points are not collinear. Are the points , and collinear?
(Multiple Choice)
4.8/5  (38)
(38)
Encode and Decode Messages
Encode or decode the given message, as requested, numbering the letters of the alphabet 1 through 26 in their usual
order.
-Use the coding matrix and its inverse to decode the cryptogram .
(Multiple Choice)
4.7/5  (43)
(43)
Use Cramer's rule to determine if the system is inconsistent system or contains dependent equations.
- x+z=1 2x-2y=-2 y+z=4
(Multiple Choice)
4.9/5  (43)
(43)
Determinants are used to show that three points lie on the same line (are collinear). If
-Determinants are used to show that three points lie on the same line (are collinear). If
then the points , and are collinear. If the determinant does not equal 0 , then the points are not collinear Are the points and collinear?
(Multiple Choice)
4.9/5  (31)
(31)
Apply Gaussian Elimination to Systems with More Variables than Equations
Use Gaussian elimination to find the complete solution to the system of equations, or state that none exists.
- x+y+z=9 2x-3y+4z=7
(Multiple Choice)
4.7/5  (30)
(30)
Use Cramer's rule to solve the system.
- 5x=-5y+10 4x=-y-10
(Multiple Choice)
4.7/5  (40)
(40)
Showing 121 - 140 of 152
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)