Exam 24: Gausss Law
Exam 1: Physics and Measurement25 Questions
Exam 2: Motion in One Dimension66 Questions
Exam 3: Vectors47 Questions
Exam 4: Motion in Two Dimensions79 Questions
Exam 5: The Laws of Motion113 Questions
Exam 6: Circular Motion and Other Applications of Newtons Laws55 Questions
Exam 7: Energy of a System74 Questions
Exam 8: Conservation of Energy84 Questions
Exam 9: Linear Momentum and Collisions89 Questions
Exam 10: Rotation of a Rigid Object About a Fixed Axis82 Questions
Exam 11: Angular Momentum46 Questions
Exam 12: Static Equilibrium and Elasticity34 Questions
Exam 13: Universal Gravitation47 Questions
Exam 14: Fluid Mechanics53 Questions
Exam 15: Oscillatory Motion41 Questions
Exam 16: Wave Motion82 Questions
Exam 18: Superposition and Standing Waves72 Questions
Exam 19: Temperature47 Questions
Exam 20: The First Law of Thermodynamics61 Questions
Exam 21: The Kinetic Theory of Gases38 Questions
Exam 22: Heat Engines, Entropy, and the Second Law of Thermodynamics55 Questions
Exam 23: Electric Fields67 Questions
Exam 24: Gausss Law82 Questions
Exam 25: Electric Potential111 Questions
Exam 26: Capacitance and Dielectrics63 Questions
Exam 27: Current and Resistance34 Questions
Exam 28: Direct-Current Circuits84 Questions
Exam 29: Magnetic Fields80 Questions
Exam 30: Sources of the Magnetic Field95 Questions
Exam 31: Faradays Law62 Questions
Exam 32: Inductance23 Questions
Exam 33: Alternating-Current Circuits65 Questions
Exam 34: Electromagnetic Waves40 Questions
Exam 35: The Nature of Light and the Principles of Ray Optics37 Questions
Exam 36: Image Formation43 Questions
Exam 37: Wave Optics48 Questions
Exam 38: Diffraction Patterns and Polarization47 Questions
Exam 39: Relativity34 Questions
Exam 40: Introduction to Quantum Physics48 Questions
Exam 41: Quantum Mechanics33 Questions
Exam 42: Atomic Physics59 Questions
Exam 43: Molecules and Solids46 Questions
Exam 44: Nuclear Structure89 Questions
Exam 46: Particle Physics and Cosmology34 Questions
Select questions type
When a cube is inscribed in a sphere of radius r, the length L of a side of the cube is 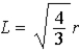 . If a positive point charge Q is placed at the center of the spherical surface, the ratio of the electric flux Φsphere at the spherical surface to the flux Φcube at the surface of the cube is
. If a positive point charge Q is placed at the center of the spherical surface, the ratio of the electric flux Φsphere at the spherical surface to the flux Φcube at the surface of the cube is
(Multiple Choice)
4.9/5  (31)
(31)
The xy plane is "painted" with a uniform surface charge density which is equal to 40 nC/m2. Consider a spherical surface with a 4.0-cm radius that has a point in the xy plane as its center. What is the electric flux through that part of the spherical surface for which z > 0?
(Multiple Choice)
4.9/5  (34)
(34)
A student has made the statement that the electric flux through one half of a Gaussian surface is always equal to the flux through the other half of the Gaussian surface. This is
(Multiple Choice)
4.8/5  (33)
(33)
Charge of uniform surface density (4.0 nC/m2) is distributed on a spherical surface (radius = 2.0 cm). What is the total electric flux through a concentric spherical surface with a radius of 4.0 cm?
(Multiple Choice)
4.9/5  (36)
(36)
A 16-nC charge is distributed uniformly along the x axis from x = 0 to x = 4 m. Which of the following integrals is correct for the magnitude (in N/C) of the electric field at x = +10 m on the x axis?
(Multiple Choice)
4.8/5  (38)
(38)
Charge of uniform density (20 nC/m2) is distributed over a cylindrical surface (radius = 1.0 cm), and a second coaxial surface (radius = 3.0 cm) carries a uniform charge density of −12 nC/m2. Determine the magnitude of the electric field at a point 4.0 cm from the symmetry axis of the two surfaces.
(Multiple Choice)
4.9/5  (34)
(34)
A uniform linear charge density of 4.0 nC/m is distributed along the entire x axis. Consider a spherical (radius = 5.0 cm) surface centered on the origin. Determine the electric flux through this surface.
(Multiple Choice)
4.8/5  (35)
(35)
Each 2.0-m length of a long cylinder (radius = 4.0 mm) has a charge of 4.0 nC distributed uniformly throughout its volume. What is the magnitude of the electric field at a point 5.0 mm from the axis of the cylinder?
(Multiple Choice)
4.9/5  (32)
(32)
A charge (uniform linear density = 9.0 nC/m) is distributed along the x axis from x = 0 to x = 3.0 m. Determine the magnitude of the electric field at a point on the x axis with x = 4.0 m.
(Multiple Choice)
4.9/5  (31)
(31)
A long cylindrical shell (radius = 2.0 cm) has a charge uniformly distributed on its surface. If the magnitude of the electric field at a point 8.0 cm radially outward from the axis of the shell is 85 N/C, how much charge is distributed on a 2.0-m length of the charged cylindrical surface?
(Multiple Choice)
4.8/5  (34)
(34)
Charge of a uniform density (8.0 nC/m2) is distributed over the entire xy plane. A charge of uniform density (3.0 nC/m2) is distributed over the parallel plane defined by z = 2.0 m. Determine the magnitude of the electric field for any point with z = 3.0 m.
(Multiple Choice)
4.9/5  (45)
(45)
Charge of uniform density (40 pC/m2) is distributed on a spherical surface (radius = 1.0 cm), and a second concentric spherical surface (radius = 3.0 cm) carries a uniform charge density of 60 pC/m2. What is the magnitude of the electric field at a point 2.0 cm from the center of the two surfaces?
(Multiple Choice)
4.8/5  (38)
(38)
Charge of uniform surface density (0.20 nC/m2) is distributed over the entire xy plane. Determine the magnitude of the electric field at any point having z = 2.0 m.
(Multiple Choice)
4.7/5  (40)
(40)
The electric flux through the two adjacent spherical surfaces shown below is known to be the same. 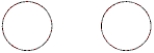 It is also known that there is no charge inside either spherical surface. We can conclude that
It is also known that there is no charge inside either spherical surface. We can conclude that
(Multiple Choice)
4.8/5  (34)
(34)
An uncharged spherical conducting shell surrounds a charge −q at the center of the shell. Then charge +3q is placed on the outside of the shell. When static equilibrium is reached, the charges on the inner and outer surfaces of the shell are respectively
(Multiple Choice)
4.9/5  (42)
(42)
A charge of uniform volume density (40 nC/m3) fills a cube with 8.0-cm edges. What is the total electric flux through the surface of this cube?
(Multiple Choice)
4.9/5  (42)
(42)
A uniformly charged rod (length = 2.0 m, charge per unit length = 5.0 nC/m) is bent to form one quadrant of a circle. What is the magnitude of the electric field at the center of the circle?
(Multiple Choice)
4.8/5  (33)
(33)
Two planes of charge with no thickness, A and B, are parallel and vertical. The electric field in the region between the two planes has magnitude 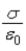 . The electric field in the region to the left of A and the electric field in the region to the right of B may have the magnitudes
. The electric field in the region to the left of A and the electric field in the region to the right of B may have the magnitudes
(Multiple Choice)
4.8/5  (35)
(35)
Charge of uniform linear density (4.0 nC/m) is distributed along the entire x axis. Determine the magnitude of the electric field on the y axis at y = 2.5 m.
(Multiple Choice)
4.8/5  (39)
(39)
The nucleus of lead-208, 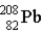 , has 82 protons within a sphere of radius 6.34 × 10−15. Each electric charge has a value of 1.60 × 10−19 C. Assuming that the protons create a spherically symmetric distribution of charge, calculate the electric field at the surface of the nucleus.
, has 82 protons within a sphere of radius 6.34 × 10−15. Each electric charge has a value of 1.60 × 10−19 C. Assuming that the protons create a spherically symmetric distribution of charge, calculate the electric field at the surface of the nucleus.
(Short Answer)
4.8/5  (42)
(42)
Showing 21 - 40 of 82
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)