The following is the list of MAD statistics for each of the models you have estimated from time-series data: \[\begin{array} { | l | r | } \hline \text { Model } & \text { MAD } \\ \hline \text { Linear Trend } & 1.38 \\ \hline \text { Quadratic Trend } & 1.29 \\ \hline \text { Exponential Trend } & 1.39 \\ \hline \text { Second-order Autoregressive } & 0.71 \\ \hline \end{array}\] Based on the MAD criterion, the most appropriate model is

A) linear trend. B) quadratic trend. C) exponential trend. D) second-order autoregressive. A) linear trend. B) quadratic trend. C) exponential trend. D) second-order autoregressive.

TABLE 16-9 Given below are Excel outputs for various estimated autoregressive models for a company's real operating revenues (in billions of dollars) from 1985 to 2008. From the data, you also know that the real operating revenues for 2006, 2007, and 2008 are 11.7909, 11.7757 and 11.5537, respectively. First-Order Autoregressive Model: \[\begin{array} { | l | r | r | r | r | } \hline & \text { Coefficients } & \begin{array} { c } \text { Standard } \\ \text { Error } \end{array} & { t \text { Stat } } & { p \text {-value } } \\ \hline \text { Intercept } & 0.1802 & 0.3980 & 0.4528 & 0.6553 \\ \hline \text { XLag1 } & 1.0112 & 0.0497 & 20.3526 & 0.0000 \\ \hline \end{array}\] Second-Order Autoregressive Model: \[\begin{array} { | l | r | r | r | r | } \hline & \text { Coefficients } & \begin{array} { c } \text { Standard } \\ \text { Error } \end{array} & t \text { Stat } & { p \text {-value } } \\ \hline \text { Intercept } & 0.3005 & 0.4408 & 0.6817 & 0.5036 \\ \hline \text { X Lag 1 } & 1.1732 & 0.2347 & 4.9980 & 0.0001 \\ \hline \mathrm { X } \text { Lag 2 } & - 0.1830 & 0.2507 & - 0.7300 & 0.4743 \\ \hline \end{array}\] Third-Order Autoregressive Model: \[\begin{array} { | l | r | r | r | r | } \hline & \text { Coefficients } &{ \begin{array} { c } \text { Standard } \\ \text { Error } \end{array} } &{ t \text { Stat } } & { p \text {-value } } \\ \hline \text { Intercept } & 0.3130 & 0.5144 & 0.6085 & 0.5509 \\ \hline \mathrm { XLag } 1 & 1.1737 & 0.2465 & 4.7617 & 0.0002 \\ \hline \mathrm { XLag } 2 & - 0.0694 & 0.3731 & - 0.1860 & 0.8547 \\ \hline \mathrm { XLag } 3 & - 0.1221 & 0.2820 & - 0.4330 & 0.6704 \\ \hline \end{array}\] -Referring to Table 16-9 and using a 5% level of significance, what is the appropriate autoregressive model for the company's real operating revenue?

A) First-Order Autoregressive Model B) Second-Order Autoregressive C) Third-Order Autoregressive D) Any of the above A) First-Order Autoregressive Model B) Second-Order Autoregressive C) Third-Order Autoregressive D) Any of the above

TABLE 16-11 The manager of a health club has recorded mean attendance in newly introduced step classes over the last 15 months: 32.1, 39.5, 40.3, 46.0, 65.2, 73.1, 83.7, 106.8, 118.0, 133.1, 163.3, 182.8, 205.6, 249.1, and 263.5. She then used Microsoft Excel to obtain the following partial output for both a first- and second-order autoregressive model. SUMMARY OUTPUT - 2nd Order Model Regression Statistics $\begin{array} { l r } \text { Multiple R } & 0.993 \\ \text { R Square } & 0.987 \\ \text { Adjusted R Square } & 0.985 \\ \text { Standard Error } & 9.276 \\ \text { Observations } & 15 \end{array}$ $\begin{array} { l c } & \text { Coefficients } \\ \text { Intercept } & 5.86 \\ \text { X Variable } 1 & 0.37 \\ \text { X Variable } 2 & 0.85 \end{array}$ SUMMARY OUTPUT - 1 st Order Model Regression Statistics $\begin{array} { l r } \text { Multiple R } & 0.993 \\ \text { R Square } & 0.987 \\ \text { Adjusted R Square } & 0.985 \\ \text { Standard Error } & 9.150 \\ \text { Observations } & 15 \end{array}$ $\begin{array} { l c } & \text { Coefficients } \\ \text { Intercept } & 5.66 \\ \text { X Variable } 1 & 1.10 \end{array}$ -Referring to Table 16-11, using the second-order model, the forecast of mean attendance for month 16 is ________.

The answer of TABLE 16-11 The manager of a health club...

Exam 16: Time-Series Forecasting

TABLE 16-5 The number of passengers arriving at San Francisco on the Amtrak cross-country express on 6 successive Mondays were: 60, 72, 96, 84, 36, and 48. -Referring to Table 16-5, exponentially smooth the number of arrivals using a smoothing constant of 0.25.

(Essay)

4.7/5

(31)

Question 21

TABLE 16-6 The president of a chain of department stores believes that her stores' total sales have been showing a linear trend since 1990. She uses Microsoft Excel to obtain the partial output below. The dependent variable is sales (in millions of dollars), while the independent variable is coded years, where 1990 is coded as 0, 1991 is coded as 1, etc. SUMMARY OUTPUT Regression Statistics Multiple R 0.604 R Square 0.365 Adjusted R Square 0.316 Standard Error 4.800 Observations 17 Coefficients Intercept 31.2 Coded Year 0.78 -Referring to Table 16-6, the fitted trend value (in millions of dollars)for 1990 is ________.

(Short Answer)

4.7/5

(33)

Question 22

TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. Month Retail Sales 1 6,594 2 6,610 3 8,174 4 9,513 5 10,595 6 10,415 7 9,949 8 9,810 9 9,637 10 9,732 11 9,214 12 9,201 The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: $\text { Linear trend model: }$ Coefficients Standard Error t Stat P-value Intercept 7950.7564 617.6342 12.8729 0.0000 Coded Month 212.6503 95.1145 2.2357 0.0494 Quadratic trend model: Coefficients Standard Error t Stat P-value Intercept 6358.2473 417.2692 15.2378 0.0000 Coded Month 1168.1558 176.3526 6.6240 0.0001 Coded Month 2 -86.8641 15.4474 -5.6232 0.0003 Exponential trend model: Coefficients Standard Error t Stat P-value Intercept 3.8912 0.0315 123.3674 0.0000 Coded Month 0.0116 0.0049 2.3957 0.0376 $\text { First-order autoregressive: }$ Coefficients Standard Error t Stat P-value Intercept 3132.0951 1287.2899 2.4331 0.0378 YLag1 0.6823 0.1398 4.8812 0.0009 Second-order autoregressive:: Coefficients Standard Error t Stat P -value Intercept 4968.5789 766.9416 6.4784 0.0003 YLag1 0.9333 0.1547 6.0316 0.0005 YLag2 -0.4487 0.1238 -3.6235 0.0085 Third-order autoregressive:: Coefficients Standard Error t Stat P-value Intercept 6782.7567 2105.7115 3.2211 0.0234 YLag1 0.5481 0.3918 1.3990 0.2207 YLag2 0.0198 0.4034 0.0490 0.9628 YLag3 -0.2749 0.2234 -1.2308 0.2731 Below is the residual plot of the various models: 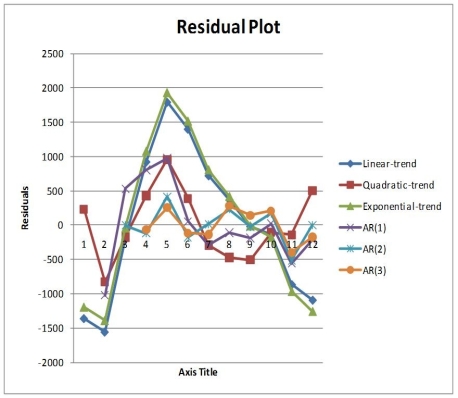$TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. \begin{array}{l} \text { Month Retail Sales }\\ \begin{array} { | c | c | } \hline 1 & 6,594 \\ \hline 2 & 6,610 \\ \hline 3 & 8,174 \\ \hline 4 & 9,513 \\ \hline 5 & 10,595 \\ \hline 6 & 10,415 \\ \hline 7 & 9,949 \\ \hline 8 & 9,810 \\ \hline 9 & 9,637 \\ \hline 10 & 9,732 \\ \hline 11 & 9,214 \\ \hline 12 & 9,201 \\ \hline \end{array} \end{array} The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: \text { Linear trend model: } \begin{array} { | l | r | r | r | r | } \hline & { \text { Coefficients } } & \text { Standard Error } & { t \text { Stat } } & { \text { P-value } } \\ \hline \text { Intercept } & 7950.7564 & 617.6342 & 12.8729 & 0.0000 \\ \hline \text { Coded Month } & 212.6503 & 95.1145 & 2.2357 & 0.0494 \\ \hline \end{array} Quadratic trend model: \begin{array}{|l|r|r|r|r|} \hline & \text { Coefficients } & \text { Standard Error } & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6358.2473 & 417.2692 & 15.2378 & 0.0000 \\ \hline \text { Coded Month } & 1168.1558 & 176.3526 & 6.6240 & 0.0001 \\ \hline \text { Coded Month 2 } & -86.8641 & 15.4474 & -5.6232 & 0.0003 \\ \hline \end{array} Exponential trend model: \begin{array}{|lrrrr} \hline & \text { Coefficients } & \text { Standard Error } &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3.8912 & 0.0315 & 123.3674 & 0.0000 \\ \hline \text { Coded Month } & 0.0116 & 0.0049 & 2.3957 & 0.0376 \\ \hline \end{array} \text { First-order autoregressive: } \begin{array}{|l|r|rrr|} \hline & {\text { Coefficients }} & {\text { Standard Error }} & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3132.0951 & 1287.2899 & 2.4331 & 0.0378 \\ \hline \text { YLag1 } & 0.6823 & 0.1398 & 4.8812 & 0.0009 \\ \hline \end{array} Second-order autoregressive:: \begin{array}{lrrrr} \hline &{\text { Coefficients }} & \text { Standard Error } &{\text { t Stat }} & {P \text {-value }} \\ \hline \text { Intercept } & 4968.5789 & 766.9416 & 6.4784 & 0.0003 \\ \hline \text { YLag1 } & 0.9333 & 0.1547 & 6.0316 & 0.0005 \\ \hline \text { YLag2 } & -0.4487 & 0.1238 & -3.6235 & 0.0085 \\ \hline \end{array} Third-order autoregressive:: \begin{array}{|l|rrrr|} \hline &{\text { Coefficients }} & {\text { Standard Error }} &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6782.7567 & 2105.7115 & 3.2211 & 0.0234 \\ \hline \text { YLag1 } & 0.5481 & 0.3918 & 1.3990 & 0.2207 \\ \hline \text { YLag2 } & 0.0198 & 0.4034 & 0.0490 & 0.9628 \\ \hline \text { YLag3 } & -0.2749 & 0.2234 & -1.2308 & 0.2731 \\ \hline \end{array} Below is the residual plot of the various models: -Referring to Table 16-13, the best model based on the residual plots is the quadratic-trend regression model.$ -Referring to Table 16-13, the best model based on the residual plots is the quadratic-trend regression model.

(True/False)

4.7/5

(39)

Question 23

The following is the list of MAD statistics for each of the models you have estimated from time-series data: Model MAD Linear Trend 1.38 Quadratic Trend 1.29 Exponential Trend 1.39 Second-order Autoregressive 0.71 Based on the MAD criterion, the most appropriate model is

(Multiple Choice)

4.8/5

(31)

Question 24

When a time series appears to be increasing at an increasing rate, such that percentage difference from value to value is constant, the appropriate model to fit is the

(Multiple Choice)

4.9/5

(39)

Question 25

TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. Month Retail Sales 1 6,594 2 6,610 3 8,174 4 9,513 5 10,595 6 10,415 7 9,949 8 9,810 9 9,637 10 9,732 11 9,214 12 9,201 The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: $\text { Linear trend model: }$ Coefficients Standard Error t Stat P-value Intercept 7950.7564 617.6342 12.8729 0.0000 Coded Month 212.6503 95.1145 2.2357 0.0494 Quadratic trend model: Coefficients Standard Error t Stat P-value Intercept 6358.2473 417.2692 15.2378 0.0000 Coded Month 1168.1558 176.3526 6.6240 0.0001 Coded Month 2 -86.8641 15.4474 -5.6232 0.0003 Exponential trend model: Coefficients Standard Error t Stat P-value Intercept 3.8912 0.0315 123.3674 0.0000 Coded Month 0.0116 0.0049 2.3957 0.0376 $\text { First-order autoregressive: }$ Coefficients Standard Error t Stat P-value Intercept 3132.0951 1287.2899 2.4331 0.0378 YLag1 0.6823 0.1398 4.8812 0.0009 Second-order autoregressive:: Coefficients Standard Error t Stat P -value Intercept 4968.5789 766.9416 6.4784 0.0003 YLag1 0.9333 0.1547 6.0316 0.0005 YLag2 -0.4487 0.1238 -3.6235 0.0085 Third-order autoregressive:: Coefficients Standard Error t Stat P-value Intercept 6782.7567 2105.7115 3.2211 0.0234 YLag1 0.5481 0.3918 1.3990 0.2207 YLag2 0.0198 0.4034 0.0490 0.9628 YLag3 -0.2749 0.2234 -1.2308 0.2731 Below is the residual plot of the various models: $TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. \begin{array}{l} \text { Month Retail Sales }\\ \begin{array} { | c | c | } \hline 1 & 6,594 \\ \hline 2 & 6,610 \\ \hline 3 & 8,174 \\ \hline 4 & 9,513 \\ \hline 5 & 10,595 \\ \hline 6 & 10,415 \\ \hline 7 & 9,949 \\ \hline 8 & 9,810 \\ \hline 9 & 9,637 \\ \hline 10 & 9,732 \\ \hline 11 & 9,214 \\ \hline 12 & 9,201 \\ \hline \end{array} \end{array} The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: \text { Linear trend model: } \begin{array} { | l | r | r | r | r | } \hline & { \text { Coefficients } } & \text { Standard Error } & { t \text { Stat } } & { \text { P-value } } \\ \hline \text { Intercept } & 7950.7564 & 617.6342 & 12.8729 & 0.0000 \\ \hline \text { Coded Month } & 212.6503 & 95.1145 & 2.2357 & 0.0494 \\ \hline \end{array} Quadratic trend model: \begin{array}{|l|r|r|r|r|} \hline & \text { Coefficients } & \text { Standard Error } & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6358.2473 & 417.2692 & 15.2378 & 0.0000 \\ \hline \text { Coded Month } & 1168.1558 & 176.3526 & 6.6240 & 0.0001 \\ \hline \text { Coded Month 2 } & -86.8641 & 15.4474 & -5.6232 & 0.0003 \\ \hline \end{array} Exponential trend model: \begin{array}{|lrrrr} \hline & \text { Coefficients } & \text { Standard Error } &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3.8912 & 0.0315 & 123.3674 & 0.0000 \\ \hline \text { Coded Month } & 0.0116 & 0.0049 & 2.3957 & 0.0376 \\ \hline \end{array} \text { First-order autoregressive: } \begin{array}{|l|r|rrr|} \hline & {\text { Coefficients }} & {\text { Standard Error }} & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3132.0951 & 1287.2899 & 2.4331 & 0.0378 \\ \hline \text { YLag1 } & 0.6823 & 0.1398 & 4.8812 & 0.0009 \\ \hline \end{array} Second-order autoregressive:: \begin{array}{lrrrr} \hline &{\text { Coefficients }} & \text { Standard Error } &{\text { t Stat }} & {P \text {-value }} \\ \hline \text { Intercept } & 4968.5789 & 766.9416 & 6.4784 & 0.0003 \\ \hline \text { YLag1 } & 0.9333 & 0.1547 & 6.0316 & 0.0005 \\ \hline \text { YLag2 } & -0.4487 & 0.1238 & -3.6235 & 0.0085 \\ \hline \end{array} Third-order autoregressive:: \begin{array}{|l|rrrr|} \hline &{\text { Coefficients }} & {\text { Standard Error }} &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6782.7567 & 2105.7115 & 3.2211 & 0.0234 \\ \hline \text { YLag1 } & 0.5481 & 0.3918 & 1.3990 & 0.2207 \\ \hline \text { YLag2 } & 0.0198 & 0.4034 & 0.0490 & 0.9628 \\ \hline \text { YLag3 } & -0.2749 & 0.2234 & -1.2308 & 0.2731 \\ \hline \end{array} Below is the residual plot of the various models: -Referring to Table 16-13, what is the p-value of the t test statistic for testing the appropriateness of the third-order autoregressive model?$ -Referring to Table 16-13, what is the p-value of the t test statistic for testing the appropriateness of the third-order autoregressive model?

(Short Answer)

4.8/5

(37)

Question 26

TABLE 16-14 A contractor developed a multiplicative time-series model to forecast the number of contracts in future quarters, using quarterly data on number of contracts during the 3-year period from 2008 to 2010. The following is the resulting regression equation: ln Ŷ = 3.37 + 0.117 X - 0.083 Q₁ + 1.28 Q₂ + 0.617 Q₃ where Ŷ is the estimated number of contracts in a quarter X is the coded quarterly value with X = 0 in the first quarter of 2008. Q₁ is a dummy variable equal to 1 in the first quarter of a year and 0 otherwise. Q₂ is a dummy variable equal to 1 in the second quarter of a year and 0 otherwise. Q₃ is a dummy variable equal to 1 in the third quarter of a year and 0 otherwise. -Referring to Table 16-14, using the regression equation, which of the following values is the best forecast for the number of contracts in the third quarter of 2011?

(Multiple Choice)

4.8/5

(38)

Question 27

TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. Month Retail Sales 1 6,594 2 6,610 3 8,174 4 9,513 5 10,595 6 10,415 7 9,949 8 9,810 9 9,637 10 9,732 11 9,214 12 9,201 The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: $\text { Linear trend model: }$ Coefficients Standard Error t Stat P-value Intercept 7950.7564 617.6342 12.8729 0.0000 Coded Month 212.6503 95.1145 2.2357 0.0494 Quadratic trend model: Coefficients Standard Error t Stat P-value Intercept 6358.2473 417.2692 15.2378 0.0000 Coded Month 1168.1558 176.3526 6.6240 0.0001 Coded Month 2 -86.8641 15.4474 -5.6232 0.0003 Exponential trend model: Coefficients Standard Error t Stat P-value Intercept 3.8912 0.0315 123.3674 0.0000 Coded Month 0.0116 0.0049 2.3957 0.0376 $\text { First-order autoregressive: }$ Coefficients Standard Error t Stat P-value Intercept 3132.0951 1287.2899 2.4331 0.0378 YLag1 0.6823 0.1398 4.8812 0.0009 Second-order autoregressive:: Coefficients Standard Error t Stat P -value Intercept 4968.5789 766.9416 6.4784 0.0003 YLag1 0.9333 0.1547 6.0316 0.0005 YLag2 -0.4487 0.1238 -3.6235 0.0085 Third-order autoregressive:: Coefficients Standard Error t Stat P-value Intercept 6782.7567 2105.7115 3.2211 0.0234 YLag1 0.5481 0.3918 1.3990 0.2207 YLag2 0.0198 0.4034 0.0490 0.9628 YLag3 -0.2749 0.2234 -1.2308 0.2731 Below is the residual plot of the various models: $TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. \begin{array}{l} \text { Month Retail Sales }\\ \begin{array} { | c | c | } \hline 1 & 6,594 \\ \hline 2 & 6,610 \\ \hline 3 & 8,174 \\ \hline 4 & 9,513 \\ \hline 5 & 10,595 \\ \hline 6 & 10,415 \\ \hline 7 & 9,949 \\ \hline 8 & 9,810 \\ \hline 9 & 9,637 \\ \hline 10 & 9,732 \\ \hline 11 & 9,214 \\ \hline 12 & 9,201 \\ \hline \end{array} \end{array} The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: \text { Linear trend model: } \begin{array} { | l | r | r | r | r | } \hline & { \text { Coefficients } } & \text { Standard Error } & { t \text { Stat } } & { \text { P-value } } \\ \hline \text { Intercept } & 7950.7564 & 617.6342 & 12.8729 & 0.0000 \\ \hline \text { Coded Month } & 212.6503 & 95.1145 & 2.2357 & 0.0494 \\ \hline \end{array} Quadratic trend model: \begin{array}{|l|r|r|r|r|} \hline & \text { Coefficients } & \text { Standard Error } & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6358.2473 & 417.2692 & 15.2378 & 0.0000 \\ \hline \text { Coded Month } & 1168.1558 & 176.3526 & 6.6240 & 0.0001 \\ \hline \text { Coded Month 2 } & -86.8641 & 15.4474 & -5.6232 & 0.0003 \\ \hline \end{array} Exponential trend model: \begin{array}{|lrrrr} \hline & \text { Coefficients } & \text { Standard Error } &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3.8912 & 0.0315 & 123.3674 & 0.0000 \\ \hline \text { Coded Month } & 0.0116 & 0.0049 & 2.3957 & 0.0376 \\ \hline \end{array} \text { First-order autoregressive: } \begin{array}{|l|r|rrr|} \hline & {\text { Coefficients }} & {\text { Standard Error }} & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3132.0951 & 1287.2899 & 2.4331 & 0.0378 \\ \hline \text { YLag1 } & 0.6823 & 0.1398 & 4.8812 & 0.0009 \\ \hline \end{array} Second-order autoregressive:: \begin{array}{lrrrr} \hline &{\text { Coefficients }} & \text { Standard Error } &{\text { t Stat }} & {P \text {-value }} \\ \hline \text { Intercept } & 4968.5789 & 766.9416 & 6.4784 & 0.0003 \\ \hline \text { YLag1 } & 0.9333 & 0.1547 & 6.0316 & 0.0005 \\ \hline \text { YLag2 } & -0.4487 & 0.1238 & -3.6235 & 0.0085 \\ \hline \end{array} Third-order autoregressive:: \begin{array}{|l|rrrr|} \hline &{\text { Coefficients }} & {\text { Standard Error }} &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6782.7567 & 2105.7115 & 3.2211 & 0.0234 \\ \hline \text { YLag1 } & 0.5481 & 0.3918 & 1.3990 & 0.2207 \\ \hline \text { YLag2 } & 0.0198 & 0.4034 & 0.0490 & 0.9628 \\ \hline \text { YLag3 } & -0.2749 & 0.2234 & -1.2308 & 0.2731 \\ \hline \end{array} Below is the residual plot of the various models: -Referring to Table 16-13, you can reject the null hypothesis for testing the appropriateness of the second-order autoregressive model at the 5% level of significance.$ -Referring to Table 16-13, you can reject the null hypothesis for testing the appropriateness of the second-order autoregressive model at the 5% level of significance.

(True/False)

4.8/5

(34)

Question 28

TABLE 16-9 Given below are Excel outputs for various estimated autoregressive models for a company's real operating revenues (in billions of dollars) from 1985 to 2008. From the data, you also know that the real operating revenues for 2006, 2007, and 2008 are 11.7909, 11.7757 and 11.5537, respectively. First-Order Autoregressive Model: Coefficients Standard Error t Stat p -value Intercept 0.1802 0.3980 0.4528 0.6553 XLag1 1.0112 0.0497 20.3526 0.0000 Second-Order Autoregressive Model: Coefficients Standard Error t Stat p -value Intercept 0.3005 0.4408 0.6817 0.5036 X Lag 1 1.1732 0.2347 4.9980 0.0001 Lag 2 -0.1830 0.2507 -0.7300 0.4743 Third-Order Autoregressive Model: Coefficients Standard Error t Stat p -value Intercept 0.3130 0.5144 0.6085 0.5509 1 1.1737 0.2465 4.7617 0.0002 2 -0.0694 0.3731 -0.1860 0.8547 3 -0.1221 0.2820 -0.4330 0.6704 -Referring to Table 16-9 and using a 5% level of significance, what is the appropriate autoregressive model for the company's real operating revenue?

(Multiple Choice)

4.9/5

(44)

Question 29

TABLE 16-11 The manager of a health club has recorded mean attendance in newly introduced step classes over the last 15 months: 32.1, 39.5, 40.3, 46.0, 65.2, 73.1, 83.7, 106.8, 118.0, 133.1, 163.3, 182.8, 205.6, 249.1, and 263.5. She then used Microsoft Excel to obtain the following partial output for both a first- and second-order autoregressive model. SUMMARY OUTPUT - 2nd Order Model Regression Statistics Multiple R 0.993 R Square 0.987 Adjusted R Square 0.985 Standard Error 9.276 Observations 15 Coefficients Intercept 5.86 X Variable 1 0.37 X Variable 2 0.85 SUMMARY OUTPUT - 1 st Order Model Regression Statistics Multiple R 0.993 R Square 0.987 Adjusted R Square 0.985 Standard Error 9.150 Observations 15 Coefficients Intercept 5.66 X Variable 1 1.10 -Referring to Table 16-11, using the second-order model, the forecast of mean attendance for month 16 is ________.

(Short Answer)

4.7/5

(32)

Question 30

To assess the adequacy of a forecasting model, one measure that is often used is

(Multiple Choice)

4.8/5

(39)

Question 31

TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. Month Retail Sales 1 6,594 2 6,610 3 8,174 4 9,513 5 10,595 6 10,415 7 9,949 8 9,810 9 9,637 10 9,732 11 9,214 12 9,201 The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: $\text { Linear trend model: }$ Coefficients Standard Error t Stat P-value Intercept 7950.7564 617.6342 12.8729 0.0000 Coded Month 212.6503 95.1145 2.2357 0.0494 Quadratic trend model: Coefficients Standard Error t Stat P-value Intercept 6358.2473 417.2692 15.2378 0.0000 Coded Month 1168.1558 176.3526 6.6240 0.0001 Coded Month 2 -86.8641 15.4474 -5.6232 0.0003 Exponential trend model: Coefficients Standard Error t Stat P-value Intercept 3.8912 0.0315 123.3674 0.0000 Coded Month 0.0116 0.0049 2.3957 0.0376 $\text { First-order autoregressive: }$ Coefficients Standard Error t Stat P-value Intercept 3132.0951 1287.2899 2.4331 0.0378 YLag1 0.6823 0.1398 4.8812 0.0009 Second-order autoregressive:: Coefficients Standard Error t Stat P -value Intercept 4968.5789 766.9416 6.4784 0.0003 YLag1 0.9333 0.1547 6.0316 0.0005 YLag2 -0.4487 0.1238 -3.6235 0.0085 Third-order autoregressive:: Coefficients Standard Error t Stat P-value Intercept 6782.7567 2105.7115 3.2211 0.0234 YLag1 0.5481 0.3918 1.3990 0.2207 YLag2 0.0198 0.4034 0.0490 0.9628 YLag3 -0.2749 0.2234 -1.2308 0.2731 Below is the residual plot of the various models: $TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. \begin{array}{l} \text { Month Retail Sales }\\ \begin{array} { | c | c | } \hline 1 & 6,594 \\ \hline 2 & 6,610 \\ \hline 3 & 8,174 \\ \hline 4 & 9,513 \\ \hline 5 & 10,595 \\ \hline 6 & 10,415 \\ \hline 7 & 9,949 \\ \hline 8 & 9,810 \\ \hline 9 & 9,637 \\ \hline 10 & 9,732 \\ \hline 11 & 9,214 \\ \hline 12 & 9,201 \\ \hline \end{array} \end{array} The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: \text { Linear trend model: } \begin{array} { | l | r | r | r | r | } \hline & { \text { Coefficients } } & \text { Standard Error } & { t \text { Stat } } & { \text { P-value } } \\ \hline \text { Intercept } & 7950.7564 & 617.6342 & 12.8729 & 0.0000 \\ \hline \text { Coded Month } & 212.6503 & 95.1145 & 2.2357 & 0.0494 \\ \hline \end{array} Quadratic trend model: \begin{array}{|l|r|r|r|r|} \hline & \text { Coefficients } & \text { Standard Error } & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6358.2473 & 417.2692 & 15.2378 & 0.0000 \\ \hline \text { Coded Month } & 1168.1558 & 176.3526 & 6.6240 & 0.0001 \\ \hline \text { Coded Month 2 } & -86.8641 & 15.4474 & -5.6232 & 0.0003 \\ \hline \end{array} Exponential trend model: \begin{array}{|lrrrr} \hline & \text { Coefficients } & \text { Standard Error } &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3.8912 & 0.0315 & 123.3674 & 0.0000 \\ \hline \text { Coded Month } & 0.0116 & 0.0049 & 2.3957 & 0.0376 \\ \hline \end{array} \text { First-order autoregressive: } \begin{array}{|l|r|rrr|} \hline & {\text { Coefficients }} & {\text { Standard Error }} & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3132.0951 & 1287.2899 & 2.4331 & 0.0378 \\ \hline \text { YLag1 } & 0.6823 & 0.1398 & 4.8812 & 0.0009 \\ \hline \end{array} Second-order autoregressive:: \begin{array}{lrrrr} \hline &{\text { Coefficients }} & \text { Standard Error } &{\text { t Stat }} & {P \text {-value }} \\ \hline \text { Intercept } & 4968.5789 & 766.9416 & 6.4784 & 0.0003 \\ \hline \text { YLag1 } & 0.9333 & 0.1547 & 6.0316 & 0.0005 \\ \hline \text { YLag2 } & -0.4487 & 0.1238 & -3.6235 & 0.0085 \\ \hline \end{array} Third-order autoregressive:: \begin{array}{|l|rrrr|} \hline &{\text { Coefficients }} & {\text { Standard Error }} &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6782.7567 & 2105.7115 & 3.2211 & 0.0234 \\ \hline \text { YLag1 } & 0.5481 & 0.3918 & 1.3990 & 0.2207 \\ \hline \text { YLag2 } & 0.0198 & 0.4034 & 0.0490 & 0.9628 \\ \hline \text { YLag3 } & -0.2749 & 0.2234 & -1.2308 & 0.2731 \\ \hline \end{array} Below is the residual plot of the various models: -Referring to Table 16-13, what is the exponentially smoothed forecast for the 13ᵗʰ month using a smoothing coefficient of W = 0.5 if the exponentially smooth value for the 10ᵗʰ and 11ᵗʰ month are 9,746.3672 and 9,480.1836, respectively?$ -Referring to Table 16-13, what is the exponentially smoothed forecast for the 13ᵗʰ month using a smoothing coefficient of W = 0.5 if the exponentially smooth value for the 10ᵗʰ and 11ᵗʰ month are 9,746.3672 and 9,480.1836, respectively?

(Short Answer)

4.9/5

(41)

Question 32

TABLE 16-5 The number of passengers arriving at San Francisco on the Amtrak cross-country express on 6 successive Mondays were: 60, 72, 96, 84, 36, and 48. -Referring to Table 16-5, the number of arrivals will be exponentially smoothed with a smoothing constant of 0.25. The forecast of the number of arrivals on the seventh Monday will be ________.

(Short Answer)

4.9/5

(39)

Question 33

In selecting an appropriate forecasting model, the following approach is suggested.

(Multiple Choice)

4.8/5

(43)

Question 34

TABLE 16-12 A local store developed a multiplicative time-series model to forecast its revenues in future quarters, using quarterly data on its revenues during the 4-year period from 2005 to 2009. The following is the resulting regression equation: log₁₀ $\hat Y$ = 6.102 + 0.012 X - 0.129 Q₁ - 0.054 Q₂ + 0.098 Q₃ where $\hat Y$ is the estimated number of contracts in a quarter. X is the coded quarterly value with X = 0 in the first quarter of 2005. Q₁ is a dummy variable equal to 1 in the first quarter of a year and 0 otherwise. Q₂ is a dummy variable equal to 1 in the second quarter of a year and 0 otherwise. Q₃ is a dummy variable equal to 1 in the third quarter of a year and 0 otherwise. -Referring to Table 16-12, in testing the significance of the coefficient for Q₁ in the regression equation (-0.129)which has a p-value of 0.492. Which of the following is the best interpretation of this result?

(Multiple Choice)

4.9/5

(29)

Question 35

TABLE 16-11 The manager of a health club has recorded mean attendance in newly introduced step classes over the last 15 months: 32.1, 39.5, 40.3, 46.0, 65.2, 73.1, 83.7, 106.8, 118.0, 133.1, 163.3, 182.8, 205.6, 249.1, and 263.5. She then used Microsoft Excel to obtain the following partial output for both a first- and second-order autoregressive model. SUMMARY OUTPUT - 2nd Order Model Regression Statistics Multiple R 0.993 R Square 0.987 Adjusted R Square 0.985 Standard Error 9.276 Observations 15 Coefficients Intercept 5.86 X Variable 1 0.37 X Variable 2 0.85 SUMMARY OUTPUT - 1 st Order Model Regression Statistics Multiple R 0.993 R Square 0.987 Adjusted R Square 0.985 Standard Error 9.150 Observations 15 Coefficients Intercept 5.66 X Variable 1 1.10 -Referring to Table 16-11, based on the parsimony principle, the second-order model is the better model for making forecasts.

(True/False)

4.7/5

(31)

Question 36

A trend is a persistent pattern in annual time-series data that has to be followed for several years.

(True/False)

4.9/5

(32)

Question 37

TABLE 16-5 The number of passengers arriving at San Francisco on the Amtrak cross-country express on 6 successive Mondays were: 60, 72, 96, 84, 36, and 48. -Referring to Table 16-5, the number of arrivals will be smoothed with a 5-term moving average. The last smoothed value will be ________.

(Short Answer)

4.8/5

(36)

Question 38

TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. Month Retail Sales 1 6,594 2 6,610 3 8,174 4 9,513 5 10,595 6 10,415 7 9,949 8 9,810 9 9,637 10 9,732 11 9,214 12 9,201 The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: $\text { Linear trend model: }$ Coefficients Standard Error t Stat P-value Intercept 7950.7564 617.6342 12.8729 0.0000 Coded Month 212.6503 95.1145 2.2357 0.0494 Quadratic trend model: Coefficients Standard Error t Stat P-value Intercept 6358.2473 417.2692 15.2378 0.0000 Coded Month 1168.1558 176.3526 6.6240 0.0001 Coded Month 2 -86.8641 15.4474 -5.6232 0.0003 Exponential trend model: Coefficients Standard Error t Stat P-value Intercept 3.8912 0.0315 123.3674 0.0000 Coded Month 0.0116 0.0049 2.3957 0.0376 $\text { First-order autoregressive: }$ Coefficients Standard Error t Stat P-value Intercept 3132.0951 1287.2899 2.4331 0.0378 YLag1 0.6823 0.1398 4.8812 0.0009 Second-order autoregressive:: Coefficients Standard Error t Stat P -value Intercept 4968.5789 766.9416 6.4784 0.0003 YLag1 0.9333 0.1547 6.0316 0.0005 YLag2 -0.4487 0.1238 -3.6235 0.0085 Third-order autoregressive:: Coefficients Standard Error t Stat P-value Intercept 6782.7567 2105.7115 3.2211 0.0234 YLag1 0.5481 0.3918 1.3990 0.2207 YLag2 0.0198 0.4034 0.0490 0.9628 YLag3 -0.2749 0.2234 -1.2308 0.2731 Below is the residual plot of the various models: $TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. \begin{array}{l} \text { Month Retail Sales }\\ \begin{array} { | c | c | } \hline 1 & 6,594 \\ \hline 2 & 6,610 \\ \hline 3 & 8,174 \\ \hline 4 & 9,513 \\ \hline 5 & 10,595 \\ \hline 6 & 10,415 \\ \hline 7 & 9,949 \\ \hline 8 & 9,810 \\ \hline 9 & 9,637 \\ \hline 10 & 9,732 \\ \hline 11 & 9,214 \\ \hline 12 & 9,201 \\ \hline \end{array} \end{array} The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: \text { Linear trend model: } \begin{array} { | l | r | r | r | r | } \hline & { \text { Coefficients } } & \text { Standard Error } & { t \text { Stat } } & { \text { P-value } } \\ \hline \text { Intercept } & 7950.7564 & 617.6342 & 12.8729 & 0.0000 \\ \hline \text { Coded Month } & 212.6503 & 95.1145 & 2.2357 & 0.0494 \\ \hline \end{array} Quadratic trend model: \begin{array}{|l|r|r|r|r|} \hline & \text { Coefficients } & \text { Standard Error } & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6358.2473 & 417.2692 & 15.2378 & 0.0000 \\ \hline \text { Coded Month } & 1168.1558 & 176.3526 & 6.6240 & 0.0001 \\ \hline \text { Coded Month 2 } & -86.8641 & 15.4474 & -5.6232 & 0.0003 \\ \hline \end{array} Exponential trend model: \begin{array}{|lrrrr} \hline & \text { Coefficients } & \text { Standard Error } &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3.8912 & 0.0315 & 123.3674 & 0.0000 \\ \hline \text { Coded Month } & 0.0116 & 0.0049 & 2.3957 & 0.0376 \\ \hline \end{array} \text { First-order autoregressive: } \begin{array}{|l|r|rrr|} \hline & {\text { Coefficients }} & {\text { Standard Error }} & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3132.0951 & 1287.2899 & 2.4331 & 0.0378 \\ \hline \text { YLag1 } & 0.6823 & 0.1398 & 4.8812 & 0.0009 \\ \hline \end{array} Second-order autoregressive:: \begin{array}{lrrrr} \hline &{\text { Coefficients }} & \text { Standard Error } &{\text { t Stat }} & {P \text {-value }} \\ \hline \text { Intercept } & 4968.5789 & 766.9416 & 6.4784 & 0.0003 \\ \hline \text { YLag1 } & 0.9333 & 0.1547 & 6.0316 & 0.0005 \\ \hline \text { YLag2 } & -0.4487 & 0.1238 & -3.6235 & 0.0085 \\ \hline \end{array} Third-order autoregressive:: \begin{array}{|l|rrrr|} \hline &{\text { Coefficients }} & {\text { Standard Error }} &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6782.7567 & 2105.7115 & 3.2211 & 0.0234 \\ \hline \text { YLag1 } & 0.5481 & 0.3918 & 1.3990 & 0.2207 \\ \hline \text { YLag2 } & 0.0198 & 0.4034 & 0.0490 & 0.9628 \\ \hline \text { YLag3 } & -0.2749 & 0.2234 & -1.2308 & 0.2731 \\ \hline \end{array} Below is the residual plot of the various models: -Referring to Table 16-13, what is the p-value for the t test statistic for testing the significance of the quadratic term in the quadratic-trend model?$ -Referring to Table 16-13, what is the p-value for the t test statistic for testing the significance of the quadratic term in the quadratic-trend model?

(Short Answer)

4.8/5

(37)

Question 39

In selecting a forecasting model, you should perform a residual analysis.

(True/False)

4.7/5

(44)

Question 40

Showing 21 - 40 of 168

TABLE 16-5 The number of passengers arriving at San Francisco on the Amtrak cross-country express on 6 successive Mondays were: 60, 72, 96, 84, 36, and 48. -Referring to Table 16-5, exponentially smooth the number of arrivals using a smoothing constant of 0.25.

The following is the list of MAD statistics for each of the models you have estimated from time-series data: Model MAD Linear Trend 1.38 Quadratic Trend 1.29 Exponential Trend 1.39 Second-order Autoregressive 0.71 Based on the MAD criterion, the most appropriate model is

When a time series appears to be increasing at an increasing rate, such that percentage difference from value to value is constant, the appropriate model to fit is the

To assess the adequacy of a forecasting model, one measure that is often used is

In selecting an appropriate forecasting model, the following approach is suggested.

A trend is a persistent pattern in annual time-series data that has to be followed for several years.

TABLE 16-5 The number of passengers arriving at San Francisco on the Amtrak cross-country express on 6 successive Mondays were: 60, 72, 96, 84, 36, and 48. -Referring to Table 16-5, the number of arrivals will be smoothed with a 5-term moving average. The last smoothed value will be ________.

In selecting a forecasting model, you should perform a residual analysis.

Introduction

Organizing and Visualizing Data

Numerical Descriptive Measures

Basic Probability

Discrete Probability Distributions

The Normal Distribution and Other Continuous Distributions

Sampling and Sampling Distributions

Confidence Interval Estimation

Fundamentals of Hypothesis Testing: One-Sample Tests

Two-Sample Tests

Analysis of Variance

Chi-Square Tests and Nonparametric Tests

Simple Linear Regression

Introduction to Multiple Regression

Multiple Regression Model Building

Statistical Applications in Quality Management

A Roadmap for Analyzing Data

Filters