TABLE 16-4 The number of cases of merlot wine sold by a Paso Robles winery in an 8-year period follows. \[\begin{array} { c c } \text { Year } & \text { Cases of Wine } \\ 2003 & 270 \\ 2004 & 356 \\ 2005 & 398 \\ 2006 & 456 \\ 2007 & 358 \\ 2008 & 500 \\ 2009 & 410 \\ 2010 & 376 \end{array}\] -Referring to Table 16-4, a centered 3-year moving average is to be constructed for the wine sales. The result of this process will lead to a total of ________ moving averages.

The answer of TABLE 16-4 The number of cases of merlot...

TABLE 16-3 The following table contains the number of complaints received in a department store for the first 6 months of last year. \[\begin{array} { c c } \text { Month } & \text { Complaints } \\ \hline \text { January } & 36 \\ \text { February } & 45 \\ \text { March } & 81 \\ \text { April } & 90 \\ \text { May } & 108 \\ \text { June } & 144 \end{array}\] -Referring to Table 16-3, suppose the last two smoothed values are 81 and 96 (Note: they are not). What would you forecast as the value of the time series for July?

A) 81 B) 86 C) 91 D) 96 A) 81 B) 86 C) 91 D) 96

Exam 16: Time-Series Forecasting

TABLE 16-4 The number of cases of merlot wine sold by a Paso Robles winery in an 8-year period follows. Year Cases of Wine 2003 270 2004 356 2005 398 2006 456 2007 358 2008 500 2009 410 2010 376 -Referring to Table 16-4, a centered 3-year moving average is to be constructed for the wine sales. The result of this process will lead to a total of ________ moving averages.

(Short Answer)

4.9/5

(33)

Question 41

TABLE 16-3 The following table contains the number of complaints received in a department store for the first 6 months of last year. Month Complaints January 36 February 45 March 81 April 90 May 108 June 144 -Referring to Table 16-3, suppose the last two smoothed values are 81 and 96 (Note: they are not). What would you forecast as the value of the time series for July?

(Multiple Choice)

4.9/5

(28)

Question 42

The fairly regular fluctuations that occur within each year would be contained in the ________ component.

(Multiple Choice)

4.8/5

(41)

Question 43

MAD is the summation of the residuals divided by the sample size.

(True/False)

4.8/5

(41)

Question 44

TABLE 16-6 The president of a chain of department stores believes that her stores' total sales have been showing a linear trend since 1990. She uses Microsoft Excel to obtain the partial output below. The dependent variable is sales (in millions of dollars), while the independent variable is coded years, where 1990 is coded as 0, 1991 is coded as 1, etc. SUMMARY OUTPUT Regression Statistics Multiple R 0.604 R Square 0.365 Adjusted R Square 0.316 Standard Error 4.800 Observations 17 Coefficients Intercept 31.2 Coded Year 0.78 -Referring to Table 16-6, the fitted trend value (in millions of dollars)for 1995 is ________.

(Short Answer)

4.9/5

(36)

Question 45

TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. Month Retail Sales 1 6,594 2 6,610 3 8,174 4 9,513 5 10,595 6 10,415 7 9,949 8 9,810 9 9,637 10 9,732 11 9,214 12 9,201 The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: $\text { Linear trend model: }$ Coefficients Standard Error t Stat P-value Intercept 7950.7564 617.6342 12.8729 0.0000 Coded Month 212.6503 95.1145 2.2357 0.0494 Quadratic trend model: Coefficients Standard Error t Stat P-value Intercept 6358.2473 417.2692 15.2378 0.0000 Coded Month 1168.1558 176.3526 6.6240 0.0001 Coded Month 2 -86.8641 15.4474 -5.6232 0.0003 Exponential trend model: Coefficients Standard Error t Stat P-value Intercept 3.8912 0.0315 123.3674 0.0000 Coded Month 0.0116 0.0049 2.3957 0.0376 $\text { First-order autoregressive: }$ Coefficients Standard Error t Stat P-value Intercept 3132.0951 1287.2899 2.4331 0.0378 YLag1 0.6823 0.1398 4.8812 0.0009 Second-order autoregressive:: Coefficients Standard Error t Stat P -value Intercept 4968.5789 766.9416 6.4784 0.0003 YLag1 0.9333 0.1547 6.0316 0.0005 YLag2 -0.4487 0.1238 -3.6235 0.0085 Third-order autoregressive:: Coefficients Standard Error t Stat P-value Intercept 6782.7567 2105.7115 3.2211 0.0234 YLag1 0.5481 0.3918 1.3990 0.2207 YLag2 0.0198 0.4034 0.0490 0.9628 YLag3 -0.2749 0.2234 -1.2308 0.2731 Below is the residual plot of the various models: 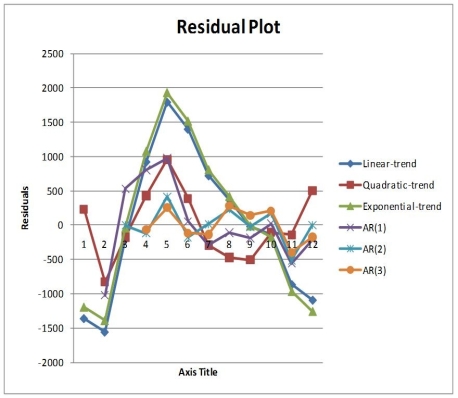$TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. \begin{array}{l} \text { Month Retail Sales }\\ \begin{array} { | c | c | } \hline 1 & 6,594 \\ \hline 2 & 6,610 \\ \hline 3 & 8,174 \\ \hline 4 & 9,513 \\ \hline 5 & 10,595 \\ \hline 6 & 10,415 \\ \hline 7 & 9,949 \\ \hline 8 & 9,810 \\ \hline 9 & 9,637 \\ \hline 10 & 9,732 \\ \hline 11 & 9,214 \\ \hline 12 & 9,201 \\ \hline \end{array} \end{array} The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: \text { Linear trend model: } \begin{array} { | l | r | r | r | r | } \hline & { \text { Coefficients } } & \text { Standard Error } & { t \text { Stat } } & { \text { P-value } } \\ \hline \text { Intercept } & 7950.7564 & 617.6342 & 12.8729 & 0.0000 \\ \hline \text { Coded Month } & 212.6503 & 95.1145 & 2.2357 & 0.0494 \\ \hline \end{array} Quadratic trend model: \begin{array}{|l|r|r|r|r|} \hline & \text { Coefficients } & \text { Standard Error } & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6358.2473 & 417.2692 & 15.2378 & 0.0000 \\ \hline \text { Coded Month } & 1168.1558 & 176.3526 & 6.6240 & 0.0001 \\ \hline \text { Coded Month 2 } & -86.8641 & 15.4474 & -5.6232 & 0.0003 \\ \hline \end{array} Exponential trend model: \begin{array}{|lrrrr} \hline & \text { Coefficients } & \text { Standard Error } &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3.8912 & 0.0315 & 123.3674 & 0.0000 \\ \hline \text { Coded Month } & 0.0116 & 0.0049 & 2.3957 & 0.0376 \\ \hline \end{array} \text { First-order autoregressive: } \begin{array}{|l|r|rrr|} \hline & {\text { Coefficients }} & {\text { Standard Error }} & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3132.0951 & 1287.2899 & 2.4331 & 0.0378 \\ \hline \text { YLag1 } & 0.6823 & 0.1398 & 4.8812 & 0.0009 \\ \hline \end{array} Second-order autoregressive:: \begin{array}{lrrrr} \hline &{\text { Coefficients }} & \text { Standard Error } &{\text { t Stat }} & {P \text {-value }} \\ \hline \text { Intercept } & 4968.5789 & 766.9416 & 6.4784 & 0.0003 \\ \hline \text { YLag1 } & 0.9333 & 0.1547 & 6.0316 & 0.0005 \\ \hline \text { YLag2 } & -0.4487 & 0.1238 & -3.6235 & 0.0085 \\ \hline \end{array} Third-order autoregressive:: \begin{array}{|l|rrrr|} \hline &{\text { Coefficients }} & {\text { Standard Error }} &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6782.7567 & 2105.7115 & 3.2211 & 0.0234 \\ \hline \text { YLag1 } & 0.5481 & 0.3918 & 1.3990 & 0.2207 \\ \hline \text { YLag2 } & 0.0198 & 0.4034 & 0.0490 & 0.9628 \\ \hline \text { YLag3 } & -0.2749 & 0.2234 & -1.2308 & 0.2731 \\ \hline \end{array} Below is the residual plot of the various models: -Referring to Table 16-13, if a five-month moving average is used to smooth this series, how many moving averages can you compute?$ -Referring to Table 16-13, if a five-month moving average is used to smooth this series, how many moving averages can you compute?

(Short Answer)

4.9/5

(28)

Question 46

TABLE 16-4 The number of cases of merlot wine sold by a Paso Robles winery in an 8-year period follows. Year Cases of Wine 2003 270 2004 356 2005 398 2006 456 2007 358 2008 500 2009 410 2010 376 -Referring to Table 16-4, a centered 3-year moving average is to be constructed for the wine sales. The moving average for 2007 is ________.

(Short Answer)

4.8/5

(40)

Question 47

TABLE 16-4 The number of cases of merlot wine sold by a Paso Robles winery in an 8-year period follows. Year Cases of Wine 2003 270 2004 356 2005 398 2006 456 2007 358 2008 500 2009 410 2010 376 -Referring to Table 16-4, construct a centered 5-year moving average for the wine sales.

(Essay)

4.8/5

(35)

Question 48

TABLE 16-14 A contractor developed a multiplicative time-series model to forecast the number of contracts in future quarters, using quarterly data on number of contracts during the 3-year period from 2008 to 2010. The following is the resulting regression equation: ln Ŷ = 3.37 + 0.117 X - 0.083 Q₁ + 1.28 Q₂ + 0.617 Q₃ where Ŷ is the estimated number of contracts in a quarter X is the coded quarterly value with X = 0 in the first quarter of 2008. Q₁ is a dummy variable equal to 1 in the first quarter of a year and 0 otherwise. Q₂ is a dummy variable equal to 1 in the second quarter of a year and 0 otherwise. Q₃ is a dummy variable equal to 1 in the third quarter of a year and 0 otherwise. -Referring to Table 16-14, the best interpretation of the coefficient of X (0.117)in the regression equation is

(Multiple Choice)

4.8/5

(44)

Question 49

TABLE 16-10 Business closures in Laramie, Wyoming from 2005 to 2010 were: 2005 10 2006 11 2007 13 2008 19 2009 24 2010 35 Microsoft Excel was used to fit both first-order and second-order autoregressive models, resulting in the following partial outputs: SUMMARY OUTPUT - 2nd Order Model Coefficient Intercept -5.77 X Variable 1 0.80 X Variable 2 1.14 SUMMARY OUTPUT - 1 st Order Model Coefficients Intercept -4.16 X Variable 1 1.59 -Referring to Table 16-10, the values of the MAD for the two models indicate that the first-order model should be used for forecasting.

(True/False)

4.9/5

(37)

Question 50

TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. Month Retail Sales 1 6,594 2 6,610 3 8,174 4 9,513 5 10,595 6 10,415 7 9,949 8 9,810 9 9,637 10 9,732 11 9,214 12 9,201 The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: $\text { Linear trend model: }$ Coefficients Standard Error t Stat P-value Intercept 7950.7564 617.6342 12.8729 0.0000 Coded Month 212.6503 95.1145 2.2357 0.0494 Quadratic trend model: Coefficients Standard Error t Stat P-value Intercept 6358.2473 417.2692 15.2378 0.0000 Coded Month 1168.1558 176.3526 6.6240 0.0001 Coded Month 2 -86.8641 15.4474 -5.6232 0.0003 Exponential trend model: Coefficients Standard Error t Stat P-value Intercept 3.8912 0.0315 123.3674 0.0000 Coded Month 0.0116 0.0049 2.3957 0.0376 $\text { First-order autoregressive: }$ Coefficients Standard Error t Stat P-value Intercept 3132.0951 1287.2899 2.4331 0.0378 YLag1 0.6823 0.1398 4.8812 0.0009 Second-order autoregressive:: Coefficients Standard Error t Stat P -value Intercept 4968.5789 766.9416 6.4784 0.0003 YLag1 0.9333 0.1547 6.0316 0.0005 YLag2 -0.4487 0.1238 -3.6235 0.0085 Third-order autoregressive:: Coefficients Standard Error t Stat P-value Intercept 6782.7567 2105.7115 3.2211 0.0234 YLag1 0.5481 0.3918 1.3990 0.2207 YLag2 0.0198 0.4034 0.0490 0.9628 YLag3 -0.2749 0.2234 -1.2308 0.2731 Below is the residual plot of the various models: $TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. \begin{array}{l} \text { Month Retail Sales }\\ \begin{array} { | c | c | } \hline 1 & 6,594 \\ \hline 2 & 6,610 \\ \hline 3 & 8,174 \\ \hline 4 & 9,513 \\ \hline 5 & 10,595 \\ \hline 6 & 10,415 \\ \hline 7 & 9,949 \\ \hline 8 & 9,810 \\ \hline 9 & 9,637 \\ \hline 10 & 9,732 \\ \hline 11 & 9,214 \\ \hline 12 & 9,201 \\ \hline \end{array} \end{array} The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: \text { Linear trend model: } \begin{array} { | l | r | r | r | r | } \hline & { \text { Coefficients } } & \text { Standard Error } & { t \text { Stat } } & { \text { P-value } } \\ \hline \text { Intercept } & 7950.7564 & 617.6342 & 12.8729 & 0.0000 \\ \hline \text { Coded Month } & 212.6503 & 95.1145 & 2.2357 & 0.0494 \\ \hline \end{array} Quadratic trend model: \begin{array}{|l|r|r|r|r|} \hline & \text { Coefficients } & \text { Standard Error } & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6358.2473 & 417.2692 & 15.2378 & 0.0000 \\ \hline \text { Coded Month } & 1168.1558 & 176.3526 & 6.6240 & 0.0001 \\ \hline \text { Coded Month 2 } & -86.8641 & 15.4474 & -5.6232 & 0.0003 \\ \hline \end{array} Exponential trend model: \begin{array}{|lrrrr} \hline & \text { Coefficients } & \text { Standard Error } &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3.8912 & 0.0315 & 123.3674 & 0.0000 \\ \hline \text { Coded Month } & 0.0116 & 0.0049 & 2.3957 & 0.0376 \\ \hline \end{array} \text { First-order autoregressive: } \begin{array}{|l|r|rrr|} \hline & {\text { Coefficients }} & {\text { Standard Error }} & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3132.0951 & 1287.2899 & 2.4331 & 0.0378 \\ \hline \text { YLag1 } & 0.6823 & 0.1398 & 4.8812 & 0.0009 \\ \hline \end{array} Second-order autoregressive:: \begin{array}{lrrrr} \hline &{\text { Coefficients }} & \text { Standard Error } &{\text { t Stat }} & {P \text {-value }} \\ \hline \text { Intercept } & 4968.5789 & 766.9416 & 6.4784 & 0.0003 \\ \hline \text { YLag1 } & 0.9333 & 0.1547 & 6.0316 & 0.0005 \\ \hline \text { YLag2 } & -0.4487 & 0.1238 & -3.6235 & 0.0085 \\ \hline \end{array} Third-order autoregressive:: \begin{array}{|l|rrrr|} \hline &{\text { Coefficients }} & {\text { Standard Error }} &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6782.7567 & 2105.7115 & 3.2211 & 0.0234 \\ \hline \text { YLag1 } & 0.5481 & 0.3918 & 1.3990 & 0.2207 \\ \hline \text { YLag2 } & 0.0198 & 0.4034 & 0.0490 & 0.9628 \\ \hline \text { YLag3 } & -0.2749 & 0.2234 & -1.2308 & 0.2731 \\ \hline \end{array} Below is the residual plot of the various models: -Referring to Table 16-13, what is the p-value of the t test statistic for testing the appropriateness of the second-order autoregressive model?$ -Referring to Table 16-13, what is the p-value of the t test statistic for testing the appropriateness of the second-order autoregressive model?

(Short Answer)

4.8/5

(44)

Question 51

TABLE 16-12 A local store developed a multiplicative time-series model to forecast its revenues in future quarters, using quarterly data on its revenues during the 4-year period from 2005 to 2009. The following is the resulting regression equation: log₁₀ $\hat Y$ = 6.102 + 0.012 X - 0.129 Q₁ - 0.054 Q₂ + 0.098 Q₃ where $\hat Y$ is the estimated number of contracts in a quarter. X is the coded quarterly value with X = 0 in the first quarter of 2005. Q₁ is a dummy variable equal to 1 in the first quarter of a year and 0 otherwise. Q₂ is a dummy variable equal to 1 in the second quarter of a year and 0 otherwise. Q₃ is a dummy variable equal to 1 in the third quarter of a year and 0 otherwise. -Referring to Table 16-12, to obtain a forecast for the third quarter of 2010 using the model, which of the following sets of values should be used in the regression equation?

(Multiple Choice)

4.9/5

(37)

Question 52

TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. Month Retail Sales 1 6,594 2 6,610 3 8,174 4 9,513 5 10,595 6 10,415 7 9,949 8 9,810 9 9,637 10 9,732 11 9,214 12 9,201 The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: $\text { Linear trend model: }$ Coefficients Standard Error t Stat P-value Intercept 7950.7564 617.6342 12.8729 0.0000 Coded Month 212.6503 95.1145 2.2357 0.0494 Quadratic trend model: Coefficients Standard Error t Stat P-value Intercept 6358.2473 417.2692 15.2378 0.0000 Coded Month 1168.1558 176.3526 6.6240 0.0001 Coded Month 2 -86.8641 15.4474 -5.6232 0.0003 Exponential trend model: Coefficients Standard Error t Stat P-value Intercept 3.8912 0.0315 123.3674 0.0000 Coded Month 0.0116 0.0049 2.3957 0.0376 $\text { First-order autoregressive: }$ Coefficients Standard Error t Stat P-value Intercept 3132.0951 1287.2899 2.4331 0.0378 YLag1 0.6823 0.1398 4.8812 0.0009 Second-order autoregressive:: Coefficients Standard Error t Stat P -value Intercept 4968.5789 766.9416 6.4784 0.0003 YLag1 0.9333 0.1547 6.0316 0.0005 YLag2 -0.4487 0.1238 -3.6235 0.0085 Third-order autoregressive:: Coefficients Standard Error t Stat P-value Intercept 6782.7567 2105.7115 3.2211 0.0234 YLag1 0.5481 0.3918 1.3990 0.2207 YLag2 0.0198 0.4034 0.0490 0.9628 YLag3 -0.2749 0.2234 -1.2308 0.2731 Below is the residual plot of the various models: $TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. \begin{array}{l} \text { Month Retail Sales }\\ \begin{array} { | c | c | } \hline 1 & 6,594 \\ \hline 2 & 6,610 \\ \hline 3 & 8,174 \\ \hline 4 & 9,513 \\ \hline 5 & 10,595 \\ \hline 6 & 10,415 \\ \hline 7 & 9,949 \\ \hline 8 & 9,810 \\ \hline 9 & 9,637 \\ \hline 10 & 9,732 \\ \hline 11 & 9,214 \\ \hline 12 & 9,201 \\ \hline \end{array} \end{array} The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: \text { Linear trend model: } \begin{array} { | l | r | r | r | r | } \hline & { \text { Coefficients } } & \text { Standard Error } & { t \text { Stat } } & { \text { P-value } } \\ \hline \text { Intercept } & 7950.7564 & 617.6342 & 12.8729 & 0.0000 \\ \hline \text { Coded Month } & 212.6503 & 95.1145 & 2.2357 & 0.0494 \\ \hline \end{array} Quadratic trend model: \begin{array}{|l|r|r|r|r|} \hline & \text { Coefficients } & \text { Standard Error } & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6358.2473 & 417.2692 & 15.2378 & 0.0000 \\ \hline \text { Coded Month } & 1168.1558 & 176.3526 & 6.6240 & 0.0001 \\ \hline \text { Coded Month 2 } & -86.8641 & 15.4474 & -5.6232 & 0.0003 \\ \hline \end{array} Exponential trend model: \begin{array}{|lrrrr} \hline & \text { Coefficients } & \text { Standard Error } &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3.8912 & 0.0315 & 123.3674 & 0.0000 \\ \hline \text { Coded Month } & 0.0116 & 0.0049 & 2.3957 & 0.0376 \\ \hline \end{array} \text { First-order autoregressive: } \begin{array}{|l|r|rrr|} \hline & {\text { Coefficients }} & {\text { Standard Error }} & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3132.0951 & 1287.2899 & 2.4331 & 0.0378 \\ \hline \text { YLag1 } & 0.6823 & 0.1398 & 4.8812 & 0.0009 \\ \hline \end{array} Second-order autoregressive:: \begin{array}{lrrrr} \hline &{\text { Coefficients }} & \text { Standard Error } &{\text { t Stat }} & {P \text {-value }} \\ \hline \text { Intercept } & 4968.5789 & 766.9416 & 6.4784 & 0.0003 \\ \hline \text { YLag1 } & 0.9333 & 0.1547 & 6.0316 & 0.0005 \\ \hline \text { YLag2 } & -0.4487 & 0.1238 & -3.6235 & 0.0085 \\ \hline \end{array} Third-order autoregressive:: \begin{array}{|l|rrrr|} \hline &{\text { Coefficients }} & {\text { Standard Error }} &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6782.7567 & 2105.7115 & 3.2211 & 0.0234 \\ \hline \text { YLag1 } & 0.5481 & 0.3918 & 1.3990 & 0.2207 \\ \hline \text { YLag2 } & 0.0198 & 0.4034 & 0.0490 & 0.9628 \\ \hline \text { YLag3 } & -0.2749 & 0.2234 & -1.2308 & 0.2731 \\ \hline \end{array} Below is the residual plot of the various models: -Referring to Table 16-13, the best model based on the residual plots is the linear-trend model.$ -Referring to Table 16-13, the best model based on the residual plots is the linear-trend model.

(True/False)

4.8/5

(30)

Question 53

TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. Month Retail Sales 1 6,594 2 6,610 3 8,174 4 9,513 5 10,595 6 10,415 7 9,949 8 9,810 9 9,637 10 9,732 11 9,214 12 9,201 The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: $\text { Linear trend model: }$ Coefficients Standard Error t Stat P-value Intercept 7950.7564 617.6342 12.8729 0.0000 Coded Month 212.6503 95.1145 2.2357 0.0494 Quadratic trend model: Coefficients Standard Error t Stat P-value Intercept 6358.2473 417.2692 15.2378 0.0000 Coded Month 1168.1558 176.3526 6.6240 0.0001 Coded Month 2 -86.8641 15.4474 -5.6232 0.0003 Exponential trend model: Coefficients Standard Error t Stat P-value Intercept 3.8912 0.0315 123.3674 0.0000 Coded Month 0.0116 0.0049 2.3957 0.0376 $\text { First-order autoregressive: }$ Coefficients Standard Error t Stat P-value Intercept 3132.0951 1287.2899 2.4331 0.0378 YLag1 0.6823 0.1398 4.8812 0.0009 Second-order autoregressive:: Coefficients Standard Error t Stat P -value Intercept 4968.5789 766.9416 6.4784 0.0003 YLag1 0.9333 0.1547 6.0316 0.0005 YLag2 -0.4487 0.1238 -3.6235 0.0085 Third-order autoregressive:: Coefficients Standard Error t Stat P-value Intercept 6782.7567 2105.7115 3.2211 0.0234 YLag1 0.5481 0.3918 1.3990 0.2207 YLag2 0.0198 0.4034 0.0490 0.9628 YLag3 -0.2749 0.2234 -1.2308 0.2731 Below is the residual plot of the various models: $TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. \begin{array}{l} \text { Month Retail Sales }\\ \begin{array} { | c | c | } \hline 1 & 6,594 \\ \hline 2 & 6,610 \\ \hline 3 & 8,174 \\ \hline 4 & 9,513 \\ \hline 5 & 10,595 \\ \hline 6 & 10,415 \\ \hline 7 & 9,949 \\ \hline 8 & 9,810 \\ \hline 9 & 9,637 \\ \hline 10 & 9,732 \\ \hline 11 & 9,214 \\ \hline 12 & 9,201 \\ \hline \end{array} \end{array} The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: \text { Linear trend model: } \begin{array} { | l | r | r | r | r | } \hline & { \text { Coefficients } } & \text { Standard Error } & { t \text { Stat } } & { \text { P-value } } \\ \hline \text { Intercept } & 7950.7564 & 617.6342 & 12.8729 & 0.0000 \\ \hline \text { Coded Month } & 212.6503 & 95.1145 & 2.2357 & 0.0494 \\ \hline \end{array} Quadratic trend model: \begin{array}{|l|r|r|r|r|} \hline & \text { Coefficients } & \text { Standard Error } & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6358.2473 & 417.2692 & 15.2378 & 0.0000 \\ \hline \text { Coded Month } & 1168.1558 & 176.3526 & 6.6240 & 0.0001 \\ \hline \text { Coded Month 2 } & -86.8641 & 15.4474 & -5.6232 & 0.0003 \\ \hline \end{array} Exponential trend model: \begin{array}{|lrrrr} \hline & \text { Coefficients } & \text { Standard Error } &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3.8912 & 0.0315 & 123.3674 & 0.0000 \\ \hline \text { Coded Month } & 0.0116 & 0.0049 & 2.3957 & 0.0376 \\ \hline \end{array} \text { First-order autoregressive: } \begin{array}{|l|r|rrr|} \hline & {\text { Coefficients }} & {\text { Standard Error }} & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3132.0951 & 1287.2899 & 2.4331 & 0.0378 \\ \hline \text { YLag1 } & 0.6823 & 0.1398 & 4.8812 & 0.0009 \\ \hline \end{array} Second-order autoregressive:: \begin{array}{lrrrr} \hline &{\text { Coefficients }} & \text { Standard Error } &{\text { t Stat }} & {P \text {-value }} \\ \hline \text { Intercept } & 4968.5789 & 766.9416 & 6.4784 & 0.0003 \\ \hline \text { YLag1 } & 0.9333 & 0.1547 & 6.0316 & 0.0005 \\ \hline \text { YLag2 } & -0.4487 & 0.1238 & -3.6235 & 0.0085 \\ \hline \end{array} Third-order autoregressive:: \begin{array}{|l|rrrr|} \hline &{\text { Coefficients }} & {\text { Standard Error }} &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6782.7567 & 2105.7115 & 3.2211 & 0.0234 \\ \hline \text { YLag1 } & 0.5481 & 0.3918 & 1.3990 & 0.2207 \\ \hline \text { YLag2 } & 0.0198 & 0.4034 & 0.0490 & 0.9628 \\ \hline \text { YLag3 } & -0.2749 & 0.2234 & -1.2308 & 0.2731 \\ \hline \end{array} Below is the residual plot of the various models: -Referring to Table 16-13, you can conclude that the quadratic term in the quadratic-trend model is statistically significant at the 5% level of significance.$ -Referring to Table 16-13, you can conclude that the quadratic term in the quadratic-trend model is statistically significant at the 5% level of significance.

(True/False)

4.8/5

(35)

Question 54

TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. Month Retail Sales 1 6,594 2 6,610 3 8,174 4 9,513 5 10,595 6 10,415 7 9,949 8 9,810 9 9,637 10 9,732 11 9,214 12 9,201 The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: $\text { Linear trend model: }$ Coefficients Standard Error t Stat P-value Intercept 7950.7564 617.6342 12.8729 0.0000 Coded Month 212.6503 95.1145 2.2357 0.0494 Quadratic trend model: Coefficients Standard Error t Stat P-value Intercept 6358.2473 417.2692 15.2378 0.0000 Coded Month 1168.1558 176.3526 6.6240 0.0001 Coded Month 2 -86.8641 15.4474 -5.6232 0.0003 Exponential trend model: Coefficients Standard Error t Stat P-value Intercept 3.8912 0.0315 123.3674 0.0000 Coded Month 0.0116 0.0049 2.3957 0.0376 $\text { First-order autoregressive: }$ Coefficients Standard Error t Stat P-value Intercept 3132.0951 1287.2899 2.4331 0.0378 YLag1 0.6823 0.1398 4.8812 0.0009 Second-order autoregressive:: Coefficients Standard Error t Stat P -value Intercept 4968.5789 766.9416 6.4784 0.0003 YLag1 0.9333 0.1547 6.0316 0.0005 YLag2 -0.4487 0.1238 -3.6235 0.0085 Third-order autoregressive:: Coefficients Standard Error t Stat P-value Intercept 6782.7567 2105.7115 3.2211 0.0234 YLag1 0.5481 0.3918 1.3990 0.2207 YLag2 0.0198 0.4034 0.0490 0.9628 YLag3 -0.2749 0.2234 -1.2308 0.2731 Below is the residual plot of the various models: $TABLE 16-13 Given below is the monthly time-series data for U.S. retail sales of building materials over a specific year. \begin{array}{l} \text { Month Retail Sales }\\ \begin{array} { | c | c | } \hline 1 & 6,594 \\ \hline 2 & 6,610 \\ \hline 3 & 8,174 \\ \hline 4 & 9,513 \\ \hline 5 & 10,595 \\ \hline 6 & 10,415 \\ \hline 7 & 9,949 \\ \hline 8 & 9,810 \\ \hline 9 & 9,637 \\ \hline 10 & 9,732 \\ \hline 11 & 9,214 \\ \hline 12 & 9,201 \\ \hline \end{array} \end{array} The results of the linear trend, quadratic trend, exponential trend, first-order autoregressive, second-order autoregressive and third-order autoregressive model are presented below in which the coded month for the first month is 0: \text { Linear trend model: } \begin{array} { | l | r | r | r | r | } \hline & { \text { Coefficients } } & \text { Standard Error } & { t \text { Stat } } & { \text { P-value } } \\ \hline \text { Intercept } & 7950.7564 & 617.6342 & 12.8729 & 0.0000 \\ \hline \text { Coded Month } & 212.6503 & 95.1145 & 2.2357 & 0.0494 \\ \hline \end{array} Quadratic trend model: \begin{array}{|l|r|r|r|r|} \hline & \text { Coefficients } & \text { Standard Error } & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6358.2473 & 417.2692 & 15.2378 & 0.0000 \\ \hline \text { Coded Month } & 1168.1558 & 176.3526 & 6.6240 & 0.0001 \\ \hline \text { Coded Month 2 } & -86.8641 & 15.4474 & -5.6232 & 0.0003 \\ \hline \end{array} Exponential trend model: \begin{array}{|lrrrr} \hline & \text { Coefficients } & \text { Standard Error } &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3.8912 & 0.0315 & 123.3674 & 0.0000 \\ \hline \text { Coded Month } & 0.0116 & 0.0049 & 2.3957 & 0.0376 \\ \hline \end{array} \text { First-order autoregressive: } \begin{array}{|l|r|rrr|} \hline & {\text { Coefficients }} & {\text { Standard Error }} & {t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 3132.0951 & 1287.2899 & 2.4331 & 0.0378 \\ \hline \text { YLag1 } & 0.6823 & 0.1398 & 4.8812 & 0.0009 \\ \hline \end{array} Second-order autoregressive:: \begin{array}{lrrrr} \hline &{\text { Coefficients }} & \text { Standard Error } &{\text { t Stat }} & {P \text {-value }} \\ \hline \text { Intercept } & 4968.5789 & 766.9416 & 6.4784 & 0.0003 \\ \hline \text { YLag1 } & 0.9333 & 0.1547 & 6.0316 & 0.0005 \\ \hline \text { YLag2 } & -0.4487 & 0.1238 & -3.6235 & 0.0085 \\ \hline \end{array} Third-order autoregressive:: \begin{array}{|l|rrrr|} \hline &{\text { Coefficients }} & {\text { Standard Error }} &{t \text { Stat }} & {\text { P-value }} \\ \hline \text { Intercept } & 6782.7567 & 2105.7115 & 3.2211 & 0.0234 \\ \hline \text { YLag1 } & 0.5481 & 0.3918 & 1.3990 & 0.2207 \\ \hline \text { YLag2 } & 0.0198 & 0.4034 & 0.0490 & 0.9628 \\ \hline \text { YLag3 } & -0.2749 & 0.2234 & -1.2308 & 0.2731 \\ \hline \end{array} Below is the residual plot of the various models: -Referring to Table 16-13, what is the value of the t test statistic for testing the appropriateness of the third-order autoregressive model?$ -Referring to Table 16-13, what is the value of the t test statistic for testing the appropriateness of the third-order autoregressive model?

(Short Answer)

4.9/5

(35)

Question 55

TABLE 16-5 The number of passengers arriving at San Francisco on the Amtrak cross-country express on 6 successive Mondays were: 60, 72, 96, 84, 36, and 48. -Referring to Table 16-5, the number of arrivals will be smoothed with a 3-term moving average. The first smoothed value will be ________.

(Short Answer)

4.7/5

(41)

Question 56

TABLE 16-14 A contractor developed a multiplicative time-series model to forecast the number of contracts in future quarters, using quarterly data on number of contracts during the 3-year period from 2008 to 2010. The following is the resulting regression equation: ln Ŷ = 3.37 + 0.117 X - 0.083 Q₁ + 1.28 Q₂ + 0.617 Q₃ where Ŷ is the estimated number of contracts in a quarter X is the coded quarterly value with X = 0 in the first quarter of 2008. Q₁ is a dummy variable equal to 1 in the first quarter of a year and 0 otherwise. Q₂ is a dummy variable equal to 1 in the second quarter of a year and 0 otherwise. Q₃ is a dummy variable equal to 1 in the third quarter of a year and 0 otherwise. -Referring to Table 16-14, the best interpretation of the coefficient of Q₃ (0.617)in the regression equation is

(Multiple Choice)

4.8/5

(39)

Question 57

TABLE 16-12 A local store developed a multiplicative time-series model to forecast its revenues in future quarters, using quarterly data on its revenues during the 4-year period from 2005 to 2009. The following is the resulting regression equation: log₁₀ $\hat Y$ = 6.102 + 0.012 X - 0.129 Q₁ - 0.054 Q₂ + 0.098 Q₃ where $\hat Y$ is the estimated number of contracts in a quarter. X is the coded quarterly value with X = 0 in the first quarter of 2005. Q₁ is a dummy variable equal to 1 in the first quarter of a year and 0 otherwise. Q₂ is a dummy variable equal to 1 in the second quarter of a year and 0 otherwise. Q₃ is a dummy variable equal to 1 in the third quarter of a year and 0 otherwise. -Referring to Table 16-12, in testing the significance of the coefficient of X in the regression equation (0.012)which has a p-value of 0.0000. Which of the following is the best interpretation of this result?

(Multiple Choice)

4.8/5

(30)

Question 58

TABLE 16-10 Business closures in Laramie, Wyoming from 2005 to 2010 were: 2005 10 2006 11 2007 13 2008 19 2009 24 2010 35 Microsoft Excel was used to fit both first-order and second-order autoregressive models, resulting in the following partial outputs: SUMMARY OUTPUT - 2nd Order Model Coefficient Intercept -5.77 X Variable 1 0.80 X Variable 2 1.14 SUMMARY OUTPUT - 1 st Order Model Coefficients Intercept -4.16 X Variable 1 1.59 -Referring to Table 16-10, the residuals for the second-order autoregressive model are , , , and .

(Short Answer)

4.8/5

(42)

Question 59

The cyclical component of a time series

(Multiple Choice)

4.9/5

(38)

Question 60

Showing 41 - 60 of 168

The fairly regular fluctuations that occur within each year would be contained in the ________ component.

MAD is the summation of the residuals divided by the sample size.

TABLE 16-4 The number of cases of merlot wine sold by a Paso Robles winery in an 8-year period follows. Year Cases of Wine 2003 270 2004 356 2005 398 2006 456 2007 358 2008 500 2009 410 2010 376 -Referring to Table 16-4, construct a centered 5-year moving average for the wine sales.

TABLE 16-5 The number of passengers arriving at San Francisco on the Amtrak cross-country express on 6 successive Mondays were: 60, 72, 96, 84, 36, and 48. -Referring to Table 16-5, the number of arrivals will be smoothed with a 3-term moving average. The first smoothed value will be ________.

The cyclical component of a time series

Introduction

Organizing and Visualizing Data

Numerical Descriptive Measures

Basic Probability

Discrete Probability Distributions

The Normal Distribution and Other Continuous Distributions

Sampling and Sampling Distributions

Confidence Interval Estimation

Fundamentals of Hypothesis Testing: One-Sample Tests

Two-Sample Tests

Analysis of Variance

Chi-Square Tests and Nonparametric Tests

Simple Linear Regression

Introduction to Multiple Regression

Multiple Regression Model Building

Statistical Applications in Quality Management

A Roadmap for Analyzing Data

Filters