Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Use NDER on a calculator to find the numerical derivative of the function at the specified point.
- at
(Multiple Choice)
4.9/5  (30)
(30)
Find the derivative of the function using the definition of derivative.
-
(Multiple Choice)
4.9/5  (38)
(38)
Use NINT on a calculator to find the numerical integral of the function over the specified interval.
-
Round to three decimal places.
(Multiple Choice)
4.9/5  (24)
(24)
Find the limit of the function by using direct substitution.
-
(Multiple Choice)
4.9/5  (36)
(36)
Compute the average of the RRAM and LRAM approximations to estimate the area between the graph of the function
and the x-axis over the given interval using the indicated number of subintervals. (The function is non-negative on the
given interval).
- subintervals
(Multiple Choice)
4.8/5  (34)
(34)
Find the equation of the tangent line to the curve when x has the given value.
-
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-Estimate the "RRAM" area under the graph of the function above the -axis and under the graph of the function from to . Use 5 subintervals.
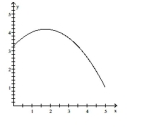
(Multiple Choice)
4.8/5  (34)
(34)
Use graphs and tables to find the limit and identify any vertical asymptotes.
-
(Multiple Choice)
4.8/5  (26)
(26)
Find the derivative of the function at the specified point.
- at
(Multiple Choice)
4.9/5  (30)
(30)
Solve the problem.
-A toy rocket is launched straight up from level ground. Its velocity function is , where is the number of seconds after launch. At what time does the rocket reach its maximum height?
(Multiple Choice)
4.9/5  (37)
(37)
Find the derivative of the function at the specified point.
- at
(Multiple Choice)
4.8/5  (30)
(30)
Solve the problem.
-The position of an object at time is given by . Find the instantaneous velocity at the indicated value of . t at
(Multiple Choice)
4.8/5  (33)
(33)
Find the derivative of the function at the specified point.
- at
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-A snail travels at feet/min for 5 minutes. How far does it travel?
(Multiple Choice)
4.8/5  (41)
(41)
Showing 101 - 120 of 167
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)