Question 1

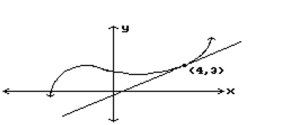
Estimate the slope of the tangent line at the indicated point.
-

Accepted Answer

A)  0 
B)  $- 1$ 
C)  Undefined 
D)  1 
A)  0 
B)  $- 1$ 
C)  Undefined 
D)  1

Question 2

Find the equation of the tangent line to the curve when x has the given value.
-$$f ( x ) = - 4 \sqrt { x } ; x = 9$$

Accepted Answer

A)  $y = - \frac { 2 } { 3 } x - 8$ 
B)  $y = \frac { 2 } { 3 } x - 6$ 
C)  $y = - \frac { 2 } { 3 } x - 6$ 
D)  $y = - \frac { 2 } { 3 } x + 6$ 
A)  $y = - \frac { 2 } { 3 } x - 8$ 
B)  $y = \frac { 2 } { 3 } x - 6$ 
C)  $y = - \frac { 2 } { 3 } x - 6$ 
D)  $y = - \frac { 2 } { 3 } x + 6$

Question 3

Solve the problem.
-Joe wants to find out how far it is across the lake. His boat has a speedometer but no odometer. The table shows the boats velocity at 10 second intervals. Estimate the distance across the lake using right-end point values.
Time Velocity

Accepted Answer

A)  $3910 \mathrm { ft }$ 
B)  $391 \mathrm { ft }$ 
C)  $4010 \mathrm { ft }$ 
D)  $5900 \mathrm { ft }$ 
A)  $3910 \mathrm { ft }$ 
B)  $391 \mathrm { ft }$ 
C)  $4010 \mathrm { ft }$ 
D)  $5900 \mathrm { ft }$

Question 4

Find the definite integral by computing an area.
-$$\int _ { 1 } ^ { 6 } 3 \mathrm { dx }$$

Accepted Answer

A)  15 
B)  $\frac { 15 } { 2 }$ 
C)  5 
D)  21 
A)  15 
B)  $\frac { 15 } { 2 }$ 
C)  5 
D)  21

Question 5

Find the definite integral by computing an area.
-$$\int _ { - 7 } ^ { 7 } \sqrt { 49 - x ^ { 2 } } d x$$

Accepted Answer

A)  $7 \pi$ 
B)  $49 \pi$ 
C)  $\frac { 49 } { 2 } \pi$ 
D)  49 
A)  $7 \pi$ 
B)  $49 \pi$ 
C)  $\frac { 49 } { 2 } \pi$ 
D)  49

Question 6

Use graphs and tables to find the limit and identify any vertical asymptotes.
-$$\lim _ { x \rightarrow 5 } \frac { 1 } { x ^ { 2 } - 25 }$$

Accepted Answer

A)  $1 ; x = - 5$ 
B)  The limit does not exist; no vertical asymptotes 
C)  The limit does not exist; $x = - 5$ and $x = 5$ 
D)  0 ; no vertical asymptotes 
A)  $1 ; x = - 5$ 
B)  The limit does not exist; no vertical asymptotes 
C)  The limit does not exist; $x = - 5$ and $x = 5$ 
D)  0 ; no vertical asymptotes

Question 7

Find the equation of the tangent line to the curve when x has the given value.
-$$f ( x ) = - 7 - x ^ { 2 } ; x = 1$$

Accepted Answer

A)  $y = - 2 x + - 6$ 
B)  $y = 1 x + - 6$ 
C)  $y = 2 x - - 6$ 
D)  $y = - 2 x$ 
A)  $y = - 2 x + - 6$ 
B)  $y = 1 x + - 6$ 
C)  $y = 2 x - - 6$ 
D)  $y = - 2 x$

Question 8

Solve the problem.
-A certain object moves in such a way that its velocity (in $\mathrm { m } / \mathrm { s }$ ) after time $t$ (in s) is given by $\mathrm { v } = \mathrm { t } ^ { 2 } + 2 \mathrm { t } + 12$. Find the distance traveled during the first four seconds by evaluating $\int _ { 0 } ^ { 4 } \left( t ^ { 2 } + 2 t + 12 \right)$ dt. Round to the nearest tenth.

Accepted Answer

A)  $64.0 \mathrm {~m}$ 
B)  $85.3 \mathrm {~m}$ 
C)  $37.3 \mathrm {~m}$ 
D)  $36.0 \mathrm {~m}$ 
A)  $64.0 \mathrm {~m}$ 
B)  $85.3 \mathrm {~m}$ 
C)  $37.3 \mathrm {~m}$ 
D)  $36.0 \mathrm {~m}$

Question 9

Find the limit of the function algebraically.
-$\lim _ { x \rightarrow 0 } \frac { x ^ { 3 } + 12 x ^ { 2 } - 5 x } { 5 x }$

Accepted Answer

A)  $- 1$ 
B)  Does not exist 
C)  5 
D)  0 
A)  $- 1$ 
B)  Does not exist 
C)  5 
D)  0

Question 10

Use NDER on a calculator to find the numerical derivative of the function at the specified point.
-$f ( x ) = \sin ( 8 x )$ at $x = 10$

Accepted Answer

A)  $0.8831$ 
B)  $993.8568$ 
C)  $- 993.8568$ 
D)  $- 0.8831$ 
A)  $0.8831$ 
B)  $993.8568$ 
C)  $- 993.8568$ 
D)  $- 0.8831$

Question 11

Find the indicated limit.
-$$\lim _ { x \rightarrow \infty } \frac { \cos \left( \frac { 2 } { x } \right) } { 5 + \frac { 2 } { x } }$$

Accepted Answer

A)  $\frac { 1 } { 5 }$ 
B)  0 
C)  Does not exist 
D)  $- \frac { 1 } { 5 }$ 
A)  $\frac { 1 } { 5 }$ 
B)  0 
C)  Does not exist 
D)  $- \frac { 1 } { 5 }$

Question 12

Determine the limit algebraically, if possible.
-$\lim _ { x \rightarrow 0 } \frac { - 7 x - 6 \sin x } { x }$

Accepted Answer

A)  0 
B)  $- 1$ 
C)  Does not exist 
D)  $- 13$ 
A)  0 
B)  $- 1$ 
C)  Does not exist 
D)  $- 13$

Question 13

Find the limit of the function algebraically.
-$$\lim _ { x \rightarrow 0 } \frac { - 5 + x } { x ^ { 4 } }$$

Accepted Answer

A)  5 
B)  $- 5$ 
C)  Does not exist 
D)  0 
A)  5 
B)  $- 5$ 
C)  Does not exist 
D)  0

Question 14

Compute the average of the RRAM and LRAM approximations to estimate the area between the graph of the function
and the x-axis over the given interval using the indicated number of subintervals. (The function is non-negative on the
given interval).
-$f ( x ) = 2 x ^ { 3 } + 4 ; [ 0,3 ] ; 3$ subintervals

Accepted Answer

A)  60 
B)  54 
C)  57 
D)  63 
A)  60 
B)  54 
C)  57 
D)  63

Question 15

Solve the problem.
-A city has a population density of 471 people per square mile in an area of 17 square miles. What is the population of the city?

Accepted Answer

A)  488 people 
B)  8007 people 
C)  13,007 people 
D)  471 people 
A)  488 people 
B)  8007 people 
C)  13,007 people 
D)  471 people

Question 16

Find the limit of the function algebraically.
-$$\lim _ { x \rightarrow 4 } \frac { \left| x ^ { 2 } - 16 \right| } { x + 4 }$$

Accepted Answer

A)  Does not exist 
B)  0 
C)  8 
D)  4 
A)  Does not exist 
B)  0 
C)  8 
D)  4

Question 17

Sketch a possible graph for a function f that has the stated properties.
-$$\text { The domain of } \mathrm { f } \text { is } [ - 5,5 ] \text { and the derivative is undefined at } x = - 2 \text { and at } x = 2 \text {. }$$

Accepted Answer

The answer of Sketch a possible graph for a function...

Question 18

Use graphs and tables to find the limit and identify any vertical asymptotes.
-$$\lim _ { x \rightarrow 5 ^ { - } } \frac { 1 } { x - 5 }$$

Accepted Answer

A)  $- \infty ; x = - 5$ 
B)  $- \infty ; x = 5$ 
C)  $\infty ; x = - 5$ 
D)  1 ; no vertical asymptotes 
A)  $- \infty ; x = - 5$ 
B)  $- \infty ; x = 5$ 
C)  $\infty ; x = - 5$ 
D)  1 ; no vertical asymptotes

Question 19

Use NINT on a calculator to find the numerical integral of the function over the specified interval.
-$$f ( x ) = 5 \tan x ; \left[ 0 , \frac { \pi } { 4 } \right]$$

Accepted Answer

A)  $2.73286463$ 
B)  $- 1.7328646$ 
C)  $- 0.26713537$ 
D)  $1.73286463$ 
A)  $2.73286463$ 
B)  $- 1.7328646$ 
C)  $- 0.26713537$ 
D)  $1.73286463$

Question 20

Use graphs and tables to find the limit and identify any vertical asymptotes.
-$$\lim _ { x \rightarrow 3 ^ { + } } \frac { x } { x + 3 }$$

Accepted Answer

A)  $- \infty ; x = 3$ 
B)  $\infty ; x = 3$ 
C)  3 ; no vertical asymptotes 
D)  $- \infty ; x = - 3$ 
A)  $- \infty ; x = 3$ 
B)  $\infty ; x = 3$ 
C)  3 ; no vertical asymptotes 
D)  $- \infty ; x = - 3$

Estimate the slope of the tangent line at the indicated point. -

Find the equation of the tangent line to the curve when x has the given value. - $f ( x ) = - 4 \sqrt { x } ; x = 9$

Solve the problem. -Joe wants to find out how far it is across the lake. His boat has a speedometer but no odometer. The table shows the boats velocity at 10 second intervals. Estimate the distance across the lake using right-end point values. Time Velocity

Find the definite integral by computing an area. - $\int _ { 1 } ^ { 6 } 3 \mathrm { dx }$

Find the definite integral by computing an area. - $\int _ { - 7 } ^ { 7 } \sqrt { 49 - x ^ { 2 } } d x$

Use graphs and tables to find the limit and identify any vertical asymptotes. - $\lim _ { x \rightarrow 5 } \frac { 1 } { x ^ { 2 } - 25 }$

Find the equation of the tangent line to the curve when x has the given value. - $f ( x ) = - 7 - x ^ { 2 } ; x = 1$

Find the limit of the function algebraically. - $\lim _ { x \rightarrow 0 } \frac { x ^ { 3 } + 12 x ^ { 2 } - 5 x } { 5 x }$

Use NDER on a calculator to find the numerical derivative of the function at the specified point. - $f ( x ) = \sin ( 8 x )$ at $x = 10$

Find the indicated limit. - $\lim _ { x \rightarrow \infty } \frac { \cos \left( \frac { 2 } { x } \right) } { 5 + \frac { 2 } { x } }$

Determine the limit algebraically, if possible. - $\lim _ { x \rightarrow 0 } \frac { - 7 x - 6 \sin x } { x }$

Find the limit of the function algebraically. - $\lim _ { x \rightarrow 0 } \frac { - 5 + x } { x ^ { 4 } }$

Solve the problem. -A city has a population density of 471 people per square mile in an area of 17 square miles. What is the population of the city?

Find the limit of the function algebraically. - $\lim _ { x \rightarrow 4 } \frac { \left| x ^ { 2 } - 16 \right| } { x + 4 }$

Use graphs and tables to find the limit and identify any vertical asymptotes. - $\lim _ { x \rightarrow 5 ^ { - } } \frac { 1 } { x - 5 }$

Use NINT on a calculator to find the numerical integral of the function over the specified interval. - $f ( x ) = 5 \tan x ; \left[ 0 , \frac { \pi } { 4 } \right]$

Use graphs and tables to find the limit and identify any vertical asymptotes. - $\lim _ { x \rightarrow 3 ^ { + } } \frac { x } { x + 3 }$

Functions and Graphs

Polynomial, Power, and Rational Functions

Exponential, Logistic, and Logarithmic Functions

Trigonometric Functions

Analytic Trigonometry

Applications of Trigonometry

Systems and Matrices

Analytic Geometry in Two and Three Dimensions

Discrete Mathematics

Statistics and Probability

Prerequisites

Filters

Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals

Estimate the slope of the tangent line at the indicated point. -

Find the equation of the tangent line to the curve when x has the given value. - f(x)=−4x;x=9f ( x ) = - 4 \sqrt { x } ; x = 9f(x)=−4x​;x=9

Solve the problem. -Joe wants to find out how far it is across the lake. His boat has a speedometer but no odometer. The table shows the boats velocity at 10 second intervals. Estimate the distance across the lake using right-end point values. Time Velocity

Find the definite integral by computing an area. - ∫163dx\int _ { 1 } ^ { 6 } 3 \mathrm { dx }∫16​3dx

Find the definite integral by computing an area. - ∫−7749−x2dx\int _ { - 7 } ^ { 7 } \sqrt { 49 - x ^ { 2 } } d x∫−77​49−x2​dx

Use graphs and tables to find the limit and identify any vertical asymptotes. - lim⁡x→51x2−25\lim _ { x \rightarrow 5 } \frac { 1 } { x ^ { 2 } - 25 }limx→5​x2−251​

Find the equation of the tangent line to the curve when x has the given value. - f(x)=−7−x2;x=1f ( x ) = - 7 - x ^ { 2 } ; x = 1f(x)=−7−x2;x=1

Find the limit of the function algebraically. - lim⁡x→0x3+12x2−5x5x\lim _ { x \rightarrow 0 } \frac { x ^ { 3 } + 12 x ^ { 2 } - 5 x } { 5 x }limx→0​5xx3+12x2−5x​

Use NDER on a calculator to find the numerical derivative of the function at the specified point. - f(x)=sin⁡(8x)f ( x ) = \sin ( 8 x )f(x)=sin(8x) at x=10x = 10x=10

Find the indicated limit. - lim⁡x→∞cos⁡(2x)5+2x\lim _ { x \rightarrow \infty } \frac { \cos \left( \frac { 2 } { x } \right) } { 5 + \frac { 2 } { x } }limx→∞​5+x2​cos(x2​)​

Determine the limit algebraically, if possible. - lim⁡x→0−7x−6sin⁡xx\lim _ { x \rightarrow 0 } \frac { - 7 x - 6 \sin x } { x }limx→0​x−7x−6sinx​

Find the limit of the function algebraically. - lim⁡x→0−5+xx4\lim _ { x \rightarrow 0 } \frac { - 5 + x } { x ^ { 4 } }limx→0​x4−5+x​