Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Solve the problem.
-An industrial ventilation system can move 2000 cubic feet per minute. How many cubic feet of air are moved in 8 hours?
(Multiple Choice)
4.7/5  (31)
(31)
Find the derivative of the function at the specified point.
- at
(Multiple Choice)
4.8/5  (34)
(34)
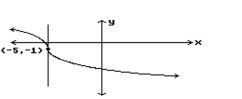
Estimate the slope of the tangent line at the indicated point.
-
(Multiple Choice)
4.7/5  (29)
(29)
Use NDER on a calculator to find the numerical derivative of the function at the specified point.
- at
(Multiple Choice)
4.9/5  (30)
(30)
Find the derivative of the function using the definition of derivative.
-
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-An arrow is shot straight up from level ground. The distance (in meters) of the arrow above the ground (the position function) is at any time (in sec). Find and the initial velocity of the arrow.
(Multiple Choice)
4.9/5  (36)
(36)
Find the limit of the function by using direct substitution.
-
(Multiple Choice)
4.8/5  (30)
(30)
Find the derivative of the function using the definition of derivative.
-
(Multiple Choice)
4.9/5  (28)
(28)
Use a graph of the function to find the derivative of the function at the given point, if it exists.
-
(Multiple Choice)
4.9/5  (37)
(37)
Use the given graph to determine the limit, if it exists.
-
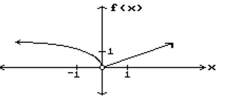
(Multiple Choice)
4.9/5  (33)
(33)
Showing 21 - 40 of 167
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)