Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Solve the problem.
-The position of an object at time is given by . Find the instantaneous velocity at the indicated value of . at
(Multiple Choice)
4.8/5  (30)
(30)
Use the given graph to determine the limit, if it exists.
-Let
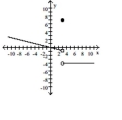
(Multiple Choice)
4.8/5  (32)
(32)
It can be shown that the area enclosed between the x-axis and one arch of the sine curve is 2. Use this fact to compute the
definite integral.
- (Hint: each rectangle is 6 times as wide.)
(Multiple Choice)
4.7/5  (42)
(42)
Use the given graph to determine the limit, if it exists.
-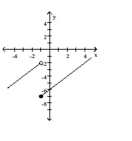 Find and .
Find and .
(Multiple Choice)
4.9/5  (36)
(36)
Use NINT on a calculator to find the numerical integral of the function over the specified interval.
-
(Multiple Choice)
4.8/5  (41)
(41)
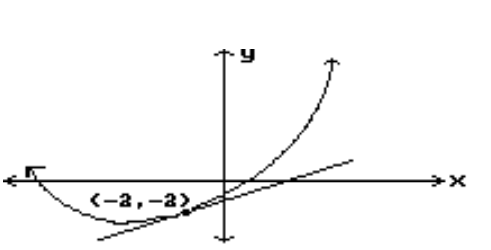
Estimate the slope of the tangent line at the indicated point.
-
(Multiple Choice)
4.7/5  (38)
(38)
It can be shown that the area enclosed between the x-axis and one arch of the sine curve is 2. Use this fact to compute the
definite integral.
-
(Multiple Choice)
4.8/5  (43)
(43)
Compute the average of the RRAM and LRAM approximations to estimate the area between the graph of the function
and the x-axis over the given interval using the indicated number of subintervals. (The function is non-negative on the
given interval).
- subintervals
(Multiple Choice)
4.8/5  (45)
(45)
Solve the problem.
-A rocket is launched straight up from level ground. The distance (in ) of the rocket above the ground (the position function) is at any time (in sec). Find and the initial velocity of the rocket.
(Multiple Choice)
4.8/5  (34)
(34)
Use the given graph to determine the limit, if it exists.
-Let
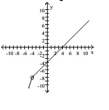
(Multiple Choice)
4.9/5  (33)
(33)
Use the given graph to determine the limit, if it exists.
-
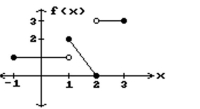
(Multiple Choice)
4.9/5  (39)
(39)
Find the limit of the function by using direct substitution.
-
(Multiple Choice)
4.8/5  (31)
(31)
Solve the problem.
-The velocity of a projectile fired straight into the air is given every half second. Use left endpoints to estimate the distance the projectile traveled in four seconds.
TimdVelocity

(Multiple Choice)
4.8/5  (36)
(36)
It can be shown that the area enclosed between the x-axis and one arch of the sine curve is 2. Use this fact to compute the
definite integral.
-
(Multiple Choice)
4.7/5  (33)
(33)
Solve the problem.
-Estimate the "RRAM" area under the graph of the function above the -axis and under the graph of the function from to . Use 5 subintervals.
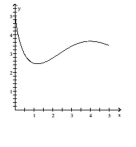
(Multiple Choice)
4.9/5  (35)
(35)
Sketch a possible graph for a function f that has the stated properties.
-
![Sketch a possible graph for a function f that has the stated properties. - \text { The domain of } \mathrm { f } \text { is } [ - 5,0 ] \text { and the derivative at } \mathrm { x } = - 2 \text { is } 3 \text {. }](https://storage.examlex.com/TB8181/11ecc52a_e3c6_1360_8347_333e4795f3a0_TB8181_11.jpg)
(Not Answered)
This question doesn't have any answer yet
Use NDER on a calculator to find the numerical derivative of the function at the specified point.
-
(Multiple Choice)
4.8/5  (29)
(29)
Use the given graph to determine the limit, if it exists.
-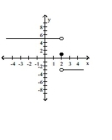 Find and .
Find and .
(Multiple Choice)
4.9/5  (30)
(30)
Showing 141 - 160 of 167
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)