Exam 2: Limits and Derivatives
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Provide an appropriate response.
-What conditions, when present, are sufficient to conclude that a function f(x) has a limit as x approaches some value of a?
(Multiple Choice)
4.8/5  (36)
(36)
Use the table of values of f to estimate the limit.
-
-5.1 -5.01 -5.001 -4.999 -4.99 -4.9 ()
(Multiple Choice)
4.8/5  (33)
(33)
Use the slopes of UQ, UR, US, and UT to estimate the rate of change of y at the specified value of x.
-x = 5 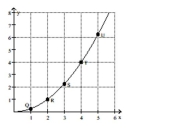
(Multiple Choice)
4.8/5  (28)
(28)
Provide an appropriate response.
-If for in , find if it exists.
(Multiple Choice)
4.9/5  (36)
(36)
Find the limit for the given function , the point , and the positive number . Then find a number such that, for all .
-f(x) = -10x - 4, L = -24, x0 = 2, and = 0.01
(Multiple Choice)
4.8/5  (41)
(41)
Provide an appropriate response.
-Given , find an interval , such that if lies in , then . What limit is being verified and what is its value?
(Multiple Choice)
4.7/5  (37)
(37)
Find the average rate of change of the function over the given interval.
-
(Multiple Choice)
4.8/5  (36)
(36)
Showing 61 - 80 of 213
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)