Exam 2: Limits and Derivatives
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Find the limit for the given function , the point , and the positive number . Then find a number such that, for all .
-
(Multiple Choice)
4.9/5  (30)
(30)
Provide an appropriate response.
-Provide a short sentence that summarizes the general limit principle given by the formal notation , given that and .
(Multiple Choice)
4.9/5  (39)
(39)
Provide an appropriate response.
-If , , and is an even function, which of the following statements are true?
I.
II.
III. does not exist.
(Multiple Choice)
4.9/5  (32)
(32)
Find the average rate of change of the function over the given interval.
-
(Multiple Choice)
4.8/5  (37)
(37)
Use a CAS to plot the function near the point x0 being approached. From your plot guess the value of the limit.
-
(Multiple Choice)
4.9/5  (31)
(31)
Provide an appropriate response.
-It can be shown that the inequalities hold for all values of . Find if it exists.
(Multiple Choice)
4.9/5  (35)
(35)
Provide an appropriate response.
-If , which of the following expressions are true?
I. does not exist.
II. does not exist.
III.
IV.
(Multiple Choice)
5.0/5  (41)
(41)
Find the limit for the given function , the point , and the positive number . Then find a number such that, for all .
-
(Multiple Choice)
4.7/5  (31)
(31)
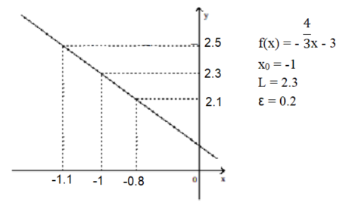
Find the limit for the given function , the point , and the positive number . Then find a number such that, for all .
-
(Multiple Choice)
4.8/5  (39)
(39)
Use a CAS to plot the function near the point x0 being approached. From your plot guess the value of the limit.
-
(Multiple Choice)
4.8/5  (39)
(39)
Find the limit for the given function , the point , and the positive number . Then find a number such that, for all .
- , and
(Multiple Choice)
4.9/5  (43)
(43)
Showing 121 - 140 of 213
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)