Exam 2: Limits and Derivatives
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Find the limit for the given function , the point , and the positive number . Then find a number such that, for all .
-
(Multiple Choice)
4.8/5  (40)
(40)
Use the table to estimate the rate of change of y at the specified value of x.
-When exposed to ethylene gas, green bananas will ripen at an accelerated rate. The number of days for ripening becomes shorter for longer exposure times. Assume that the table below gives average ripening times of
Bananas for several different ethylene exposure times:
Exposure timeRipening Time (minutes) (days) 10 4.2 15 3.5 20 2.6 25 2.1 30 1.1
Plot the data and then find a line approximating the data. With the aid of this line, find the limit of the average ripening Time as the exposure time to ethylene approaches 0. Round your answer to the nearest tenth. 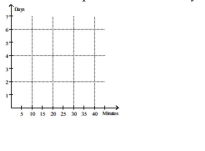
(Multiple Choice)
4.9/5  (28)
(28)
Provide an appropriate response.
-The statement "the limit of a constant times a function is the constant times the limit" follows from a combination of two fundamental limit principles. What are they?
(Multiple Choice)
4.9/5  (34)
(34)
Provide an appropriate response.
-Given , and , which of the following statements is true?
I.
II.
III. does not exist.
(Multiple Choice)
4.8/5  (38)
(38)
Find the limit for the given function , the point , and the positive number . Then find a number such that, for all .
-
(Multiple Choice)
4.8/5  (36)
(36)
Find the slope of the curve at the given point P and an equation of the tangent line at P.
-
(Multiple Choice)
4.8/5  (30)
(30)
Use the table of values of f to estimate the limit.
-
-0.1 -0.01 -0.001 0.001 0.01 0.1 ()
(Multiple Choice)
4.7/5  (35)
(35)
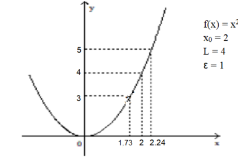
Find the limit for the given function , the point , and the positive number . Then find a number such that, for all .
-
(Multiple Choice)
4.8/5  (44)
(44)
Use a CAS to plot the function near the point x0 being approached. From your plot guess the value of the limit.
-
(Multiple Choice)
5.0/5  (35)
(35)
Showing 101 - 120 of 213
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)