Exam 2: Limits and Derivatives
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
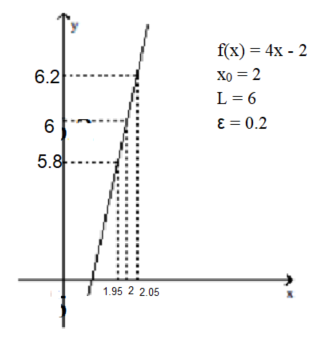
Find the limit for the given function , the point , and the positive number . Then find a number such that, for all .
-
(Multiple Choice)
4.8/5  (33)
(33)
Use a CAS to plot the function near the point x0 being approached. From your plot guess the value of the limit.
-
(Multiple Choice)
4.9/5  (35)
(35)
Use the table to estimate the rate of change of y at the specified value of x.
-x = 1.
0.900 -0.05263 0.990 -0.00503 0.999 -0.0005 1.000 0.0000 1.001 0.0005 1.010 0.00498 1.100 0.04762
(Multiple Choice)
4.8/5  (44)
(44)
Give an appropriate answer.
-Suppose and . Name the limit rules that are used to accomplish steps (a), (b), and (c) of the following calculation.
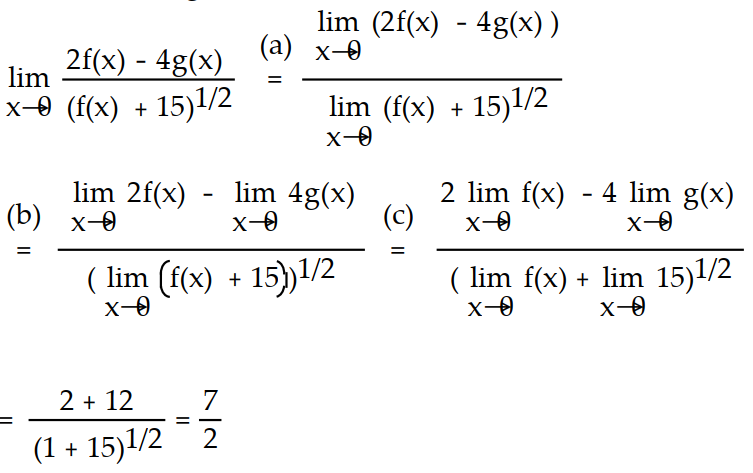
(Multiple Choice)
4.7/5  (33)
(33)
Prove the limit statement
-Ohm's Law for electrical circuits is stated , where is a constant voltage, is the resistance in ohms and is the current in amperes. Your firm has been asked to supply the resistors for a circuit in which will be 12 volts and is to be amperes. In what interval does have to lie for I to be within amps of the target value
(Multiple Choice)
4.7/5  (35)
(35)
Showing 141 - 160 of 213
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)