Exam 2: Limits and Derivatives
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Find an equation of the tangent line to the curve at the point .
Select the correct answer.
(Multiple Choice)
4.8/5  (34)
(34)
Find the equation of the tangent to the curve at the given point.
(Short Answer)
4.8/5  (41)
(41)
The mass of the part of a metal rod that lies between its left end and a point meters to the right is
Find the linear density when is .
(Short Answer)
4.9/5  (37)
(37)
Two sides of a triangle are and in length and the angle between them is increasing at a rate of . Find the rate at which the area of the triangle is increasing when the angle between the sides of fixed length is .
(Short Answer)
4.9/5  (40)
(40)
A spherical balloon is being inflated. Find the rate of increase of the surface area with respect to the radius when .
(Short Answer)
4.9/5  (34)
(34)
If is the focal length of a convex lens and an object is placed at a distance from the lens, then its image will be at a distance from the lens, where , and are related by the lens equation
Find the rate of change of with respect to .
(Multiple Choice)
4.8/5  (33)
(33)
is the position of a body moving along a coordinate line, where , and is measured in feet and in seconds.
a. Determine the time(s) and the position(s) when the body is stationary.
b. When is the body moving in the positive direction? In the negative direction?
c. Sketch a schematic showing the position of the body at any time .
(Essay)
4.7/5  (35)
(35)
Use implicit differentiation to find an equation of the tangent line to the curve at the indicated point.
(Short Answer)
4.9/5  (42)
(42)
Use differentials to estimate the amount of paint needed to apply a coat of paint thick to a hemispherical dome with diameter .
(Multiple Choice)
4.8/5  (39)
(39)
Water flows from a tank of constant cross-sectional area through an orifice of constant cross-sectional area located at the bottom of the tank. Initially, the height of the water in the tank was , and sec later it was given by the equation
How fast was the height of the water decreasing when its height was ?
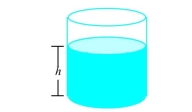
(Multiple Choice)
4.7/5  (41)
(41)
The cost (in dollars) of producing units of a certain commodity is
Find the average rate of change with respect to when the production level is changed from to .
(Multiple Choice)
5.0/5  (44)
(44)
If a snowball melts so that its surface area decreases at a rate of , find the rate at which the diameter decreases when the diameter is .
(Short Answer)
4.9/5  (36)
(36)
Use the Product Rule to find the derivative of the function. Select the correct answer.
(Multiple Choice)
4.8/5  (40)
(40)
Showing 21 - 40 of 139
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)