Exam 2: Limits and Derivatives
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Gravel is being dumped from a conveyor belt at a rate of and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is high? Round the result to the nearest hundredth.
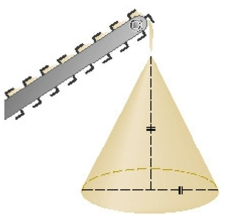
(Multiple Choice)
4.8/5  (39)
(39)
The top of a ladder slides down a vertical wall at a rate of . At the moment when the bottom of the ladder is from the wall, it slides away from the wall at a rate of . How long is the ladder?
(Short Answer)
4.8/5  (30)
(30)
is the position of a body moving along a coordinate line; is measured in feet and in seconds, where . Find the position, velocity, and speed of the body at the indicated time.
(Short Answer)
4.8/5  (39)
(39)
Use differentials to estimate the amount of paint needed to apply a coat of paint thick to a hemispherical dome with diameter .
Select the correct answer.
(Multiple Choice)
4.9/5  (32)
(32)
If is a differentiable function, find an expression for the derivative of .
(Multiple Choice)
4.8/5  (46)
(46)
Showing 121 - 139 of 139
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)